Cdtrjyty

Ссылки на статьи о тригонометрии

Тригонометрия

Обзор тригонометрии (англ.) История Использование (англ.) Функции (Обратные) Обобщённая тригонометрия (англ.)

Справочник

Тождества Точные константы (англ.) Таблицы Единичная окружность

Законы и теоремы

Теорема синусов Теорема Пифагора Теорема косинусов Теорема тангенсов Теорема котангенсов Решение треугольников

Математический анализ

Тригонометрическая подстановка (англ.) Интегралы (обратные функции) Производные (англ.)

Тригономе́трия (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю», то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии^[1]. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии (науке, исследующей размеры и форму Земли).

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.

История |

Древняя Греция |

Первые тригонометрические таблицы видимо были составлены Гиппархом, который сейчас известен как «отец тригонометрии»^[2].

Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.
Хотя в работах Евклида и Архимеда нет тригонометрии в строгом смысле этого слова, их теоремы представлены в геометрическом виде, эквивалентном специфическим тригонометрическим формулам. Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов. Для компенсации отсутствия таблицы хорд математики времен Аристарха иногда использовали хорошо известную теорему, в современной записи — sinα/sinβ < α/β < tgα/tgβ, где 0° < β < α < 90°, совместно с другими теоремами.

Первые тригонометрические таблицы были, вероятно, составлены Гиппархом Никейским (180—125 лет до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд. Возможно Гиппарх взял идею такого деления у Гипсикла, который ранее разделил день на 360 частей, хотя такое деление дня могли предложить и вавилонские астрономы.

Менелай Александрийский (100 н. э.) написал «Сферику» в трёх книгах. В первой книге он представил основы для сферических треугольников, аналогично I книге «Начал» Евклида о плоских треугольниках. Он представил теорему, для которой нет аналога у Евклида, о том, что два сферических треугольника конгруэнтны, если соответствующие углы равны, но он не делал различия между конгруэнтными и симметричными сферическими треугольниками. Другая его теорема гласит о том, что сумма углов сферического треугольника всегда больше 180°. Вторая книга «Сферики» применяет сферическую геометрию к астрономии. Третья книга содержит «теорему Менелая», известную также как «правило шести величин».

Позднее Клавдий Птолемей (90 — 168 г. н. э.) в «Альмагесте» расширил Гиппарховы «Хорды в окружности». Тринадцать книг «Альмагеста» — самая значимая тригонометрическая работа всей античности. Теорема, которая была центральной в вычислении хорд Птолемея, также известна сегодня как теорема Птолемея, которая говорит о том, что сумма произведений противоположных сторон выпуклого вписанного четырёхугольника равна произведению диагоналей. Отдельный случай теоремы Птолемея появился как 93-е предложение «Данных» Евклида.

Теорема Птолемея влечёт за собой эквивалентность четырёх формул суммы и разности для синуса и косинуса. Позднее Птолемей вывел формулу половинного угла. Птолемей использовал эти результаты для создания своих тригонометрических таблиц, хотя, возможно, эти таблицы были выведены из работ Гиппарха.

Средневековая Индия |

Замена хорд синусами стала главным достижением средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.

Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как

sin2⁡α+cos2⁡α=1,{displaystyle sin ^{2}alpha +cos ^{2}alpha =1,}

sin⁡α=cos⁡(90∘−α),{displaystyle sin alpha =cos(90^{circ }-alpha ),}

sin⁡(α±β)=sin⁡αcos⁡β±cos⁡αsin⁡β.{displaystyle sin(alpha pm beta )=sin alpha cos beta pm cos alpha sin beta .}

Индийцы также знали формулы для кратных углов sin⁡nα,cos⁡nα,{displaystyle sin nalpha ,qquad cos nalpha ,} где n=2,3,4,5.{displaystyle n=2,3,4,5.}

Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.

Южноиндийские математики в XVI веке добились больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа π. Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати^[en]» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.

С VIII века учёные стран Ближнего и Среднего Востока развили тригонометрию своих предшественников. В середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки.

Определение тригонометрических функций |

Тригонометрические функции угла θ внутри единичной окружности

Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).

• 
  Синус — отношение противолежащего катета к гипотенузе.


• 
  Косинус — отношение прилежащего катета к гипотенузе.


• 
  Тангенс — отношение противолежащего катета к прилежащему.


• 
  Котангенс — отношение прилежащего катета к противолежащему.


• 
  Секанс — отношение гипотенузы к прилежащему катету.


• 
  Косеканс — отношение гипотенузы к противолежащему катету.

Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до π2{displaystyle pi over 2} радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол θ{displaystyle theta } (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:

• 
  Синус угла θ{displaystyle theta } определяется как ордината точки A.


• 
  Косинус — абсцисса точки A.


• 
  Тангенс — отношение синуса к косинусу.


• 
  Котангенс — отношение косинуса к синусу (то есть величина, обратная тангенсу).


• 
  Секанс — величина, обратная косинусу.


• 
  Косеканс — величина, обратная синусу.

Для острых углов новые определения совпадают с прежними.

Возможно также чисто аналитическое определение этих функций, которое не связано с геометрией и представляет каждую функцию её разложением в бесконечный ряд.

Свойства функции синус |

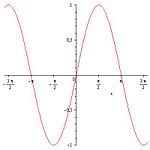
Синус

1. Область определения функции — множество всех действительных чисел: D(y)=R{displaystyle D(y)=R}.


2. Множество значений — промежуток [−1; 1]: E(y){displaystyle E(y)} = [−1;1].


3. Функция y=sin⁡(α){displaystyle y=sin left(alpha right)} является нечётной: sin⁡(−α)=−sin⁡α{displaystyle sin left(-alpha right)=-sin alpha }.


4. Функция периодическая, наименьший положительный период равен 2π{displaystyle 2pi }: sin⁡(α+2π)=sin⁡(α){displaystyle sin left(alpha +2pi right)=sin left(alpha right)}.


5. График функции пересекает ось Ох при α=πn,n∈Z{displaystyle alpha =pi n,,nin mathbb {Z} }.


6. Промежутки знакопостоянства: y>0{displaystyle y>0} при (2πn+0;π+2πn),n∈Z{displaystyle left(2pi n+0;pi +2pi nright),,nin mathbb {Z} } и y<0{displaystyle y<0} при (π+2πn;2π+2πn),n∈Z{displaystyle left(pi +2pi n;2pi +2pi nright),,nin mathbb {Z} }.


7. Функция непрерывна и имеет производную при любом значении аргумента: (sin⁡α)′=cos⁡α{displaystyle (sin alpha )'=cos alpha }
   


8. Функция y=sin⁡α{displaystyle y=sin alpha } возрастает при α∈(−π2+2πn;π2+2πn),n∈Z{displaystyle alpha in left(-{frac {pi }{2}}+2pi n;{frac {pi }{2}}+2pi nright),,nin mathbb {Z} }, и убывает при α∈(π2+2πn;3π2+2πn),n∈Z{displaystyle alpha in left({frac {pi }{2}}+2pi n;3{frac {pi }{2}}+2pi nright),,nin mathbb {Z} }.


9. Функция имеет минимум при α=−π2+2πn,n∈Z{displaystyle alpha =-{frac {pi }{2}}+2pi n,,nin mathbb {Z} } и максимум при α=π2+2πn,n∈Z{displaystyle alpha ={frac {pi }{2}}+2pi n,,nin mathbb {Z} }.

Свойства функции косинус |

Косинус

1. Область определения функции — множество всех действительных чисел: D(y)=R{displaystyle D(y)=R}.


2. Множество значений — промежуток [−1; 1]: E(y){displaystyle E(y)} = [−1;1].


3. Функция y=cos⁡(α){displaystyle y=cos left(alpha right)} является чётной: cos⁡(−α)=cos⁡α{displaystyle cos left(-alpha right)=cos alpha }.


4. Функция периодическая, наименьший положительный период равен 2π{displaystyle 2pi }: cos⁡(α+2π)=cos⁡(α){displaystyle cos left(alpha +2pi right)=cos left(alpha right)}.


5. График функции пересекает ось Ох при α=π2+πn,n∈Z{displaystyle alpha ={frac {pi }{2}}+pi n,,nin mathbb {Z} }.


6. Промежутки знакопостоянства: y>0{displaystyle y>0} при (−π2+2πn;π2+2πn),n∈Z{displaystyle left(-{frac {pi }{2}}+2pi n;{frac {pi }{2}}+2pi nright),,nin mathbb {Z} } и y<0{displaystyle y<0} при (π2+2πn;3π2+2πn),n∈Z.{displaystyle left({frac {pi }{2}}+2pi n;3{frac {pi }{2}}+2pi nright),,nin mathbb {Z} .}
   


7. Функция непрерывна и имеет производную при любом значении аргумента: (cos⁡α)′=−sin⁡α{displaystyle (cos alpha )'=-sin alpha }
   


8. Функция y=cos⁡α{displaystyle y=cos alpha } возрастает при α∈(−π+2πn;2πn),n∈Z,{displaystyle alpha in left(-pi +2pi n;2pi nright),,nin mathbb {Z} ,} и убывает при α∈(2πn;π+2πn),n∈Z.{displaystyle alpha in left(2pi n;pi +2pi nright),,nin mathbb {Z} .}
   


9. Функция имеет минимум при α=π+2πn,n∈Z{displaystyle alpha =pi +2pi n,,nin mathbb {Z} } и максимум при α=2πn,n∈Z.{displaystyle alpha =2pi n,,nin mathbb {Z} .}
   

Свойства функции тангенс |

Тангенс

1. Область определения функции — множество всех действительных чисел: D(y)=R{displaystyle D(y)=R}, кроме чисел α=π2+πn,n∈Z.{displaystyle alpha ={frac {pi }{2}}+pi n,nin mathbb {Z} ,.}
   


2. Множество значений — множество всех действительных чисел: E(y)=R.{displaystyle E(y)=R.}
   


3. Функция y=tg(α){displaystyle y=mathrm {tg} left(alpha right)} является нечётной: tg(−α)=−tg α{displaystyle mathrm {tg} left(-alpha right)=-mathrm {tg} alpha }.


4. Функция периодическая, наименьший положительный период равен π{displaystyle pi }: tg(α+π)=tg(α){displaystyle mathrm {tg} left(alpha +pi right)=mathrm {tg} left(alpha right)}.


5. График функции пересекает ось Ох при α=πn,n∈Z{displaystyle alpha =pi n,,nin mathbb {Z} }.


6. Промежутки знакопостоянства: y>0{displaystyle y>0} при (πn;π2+πn),n∈Z{displaystyle left(pi n;{frac {pi }{2}}+pi nright),,nin mathbb {Z} } и y<0{displaystyle y<0} при (−π2+πn;πn),n∈Z{displaystyle left(-{frac {pi }{2}}+pi n;pi nright),,nin mathbb {Z} }.


7. Функция непрерывна и имеет производную при любом значении аргумента из области определения: (tgx)′=1cos2⁡x.{displaystyle (mathop {operatorname {tg} } ,x)'={frac {1}{cos ^{2}x}}.}
   


8. Функция y=tg α{displaystyle y=mathrm {tg} alpha } возрастает при α∈(−π2+πn;π2+πn),n∈Z{displaystyle alpha in left(-{frac {pi }{2}}+pi n;{frac {pi }{2}}+pi nright),,nin mathbb {Z} }.

Свойства функции котангенс |

Котангенс

1. Область определения функции — множество всех действительных чисел: D(y)=R,{displaystyle D(y)=R,} кроме чисел α=πn,n∈Z.{displaystyle alpha =pi n,nin mathbb {Z} ,.}
   


2. Множество значений — множество всех действительных чисел: E(y)=R.{displaystyle E(y)=R.}
   


3. Функция y=ctg⁡(α){displaystyle y=mathop {operatorname {ctg} } left(alpha right)} является нечётной: ctg⁡(−α)=−ctg⁡ α.{displaystyle mathop {operatorname {ctg} } left(-alpha right)=-mathop {operatorname {ctg} } alpha ,.}
   


4. Функция периодическая, наименьший положительный период равен π{displaystyle pi }: ctg⁡(α+π)=ctg⁡(α).{displaystyle mathop {operatorname {ctg} } left(alpha +pi right)=mathop {operatorname {ctg} } left(alpha right).}
   


5. График функции пересекает ось Ох при α=π2+πn,n∈Z.{displaystyle alpha ={frac {pi }{2}}+pi n,,nin mathbb {Z} ,.}
   


6. Промежутки знакопостоянства: y>0{displaystyle y>0} при (πn;π2+πn),n∈Z{displaystyle left(pi n;{frac {pi }{2}}+pi nright),,nin mathbb {Z} } и y<0{displaystyle y<0} при (π2+πn;π(n+1)),n∈Z.{displaystyle left({frac {pi }{2}}+pi n;pi left(n+1right)right),,nin mathbb {Z} .}
   


7. Функция непрерывна и имеет производную при любом значении аргумента из области определения: (ctgx)′=−1sin2⁡x.{displaystyle (mathop {operatorname {ctg} } ,x)'=-{frac {1}{sin ^{2}x}}.}
   


8. Функция y=ctg⁡ α{displaystyle y=mathop {operatorname {ctg} } alpha } убывает при α∈(πn;π(n+1)),n∈Z.{displaystyle alpha in left(pi n;pi left(n+1right)right),,nin mathbb {Z} .}
   

Применение тригонометрии |

Секстант — навигационный измерительный инструмент, используемый для измерения высоты светила над горизонтом с целью определения географических координат той местности, в которой производится измерение.

Существует множество областей, в которых применяются тригонометрия и тригонометрические функции. Например, метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд, в географии для измерения расстояний между объектами, а также в спутниковых навигационных системах. Синус и косинус имеют фундаментальное значение для теории периодических функций, например при описании звуковых и световых волн.

Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов, когда требуется сферическая тригонометрия), в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятностей, в статистике, в биологии, в медицинской визуализации (например, компьютерная томография и ультразвук), в аптеках, в химии, в теории чисел (следовательно, и в криптологии), в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.

Стандартные тождества |

Тождества — это равенства, справедливые при любых значениях входящих в них переменных.

sin2⁡A+cos2⁡A=1 .{displaystyle sin ^{2}A+cos ^{2}A=1 .}

sec2⁡A−tg2A=1 .{displaystyle sec ^{2}A-{mathop {operatorname {tg} } }^{2}A=1 .}

csc2⁡A−ctg2A=1 .{displaystyle csc ^{2}A-{mathop {operatorname {ctg} } }^{2}A=1 .}

Формулы преобразования суммы углов |

sin⁡(A±B)=sin⁡A cos⁡B±cos⁡A sin⁡B.{displaystyle sin(Apm B)=sin A cos Bpm cos A sin B.}

cos⁡(A±B)=cos⁡A cos⁡B∓sin⁡A sin⁡B.{displaystyle cos(Apm B)=cos A cos Bmp sin A sin B.}

tg⁡(A±B)=tg⁡A±tg⁡B1∓tg⁡A tg⁡B.{displaystyle mathop {operatorname {tg} } (Apm B)={frac {mathop {operatorname {tg} } Apm mathop {operatorname {tg} } B}{1mp mathop {operatorname {tg} } A mathop {operatorname {tg} } B}}.}

ctg⁡(A±B)=ctg⁡A ctg⁡B∓1ctg⁡B±ctg⁡A.{displaystyle mathop {operatorname {ctg} } (Apm B)={frac {mathop {operatorname {ctg} } A mathop {operatorname {ctg} } Bmp 1}{mathop {operatorname {ctg} } Bpm mathop {operatorname {ctg} } A}}.}

Общие формулы |

Треугольник со сторонами a, b, c и соответственно противоположными углами A, B, C

В следующих тождествах, A, B и C являются углами треугольника; a, b, c — длины сторон треугольника, лежащие напротив соответствующих углов.

Теорема синусов |

Стороны треугольника пропорциональны синусам противолежащих углов. Для произвольного треугольника

asin⁡A=bsin⁡B=csin⁡C=2R,{displaystyle {frac {a}{sin A}}={frac {b}{sin B}}={frac {c}{sin C}}=2R,}

где R{displaystyle R} — радиус окружности, описанной вокруг треугольника.

R=abc(a+b+c)(a−b+c)(a+b−c)(b+c−a).{displaystyle R={frac {abc}{sqrt {(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}}.}

Теорема косинусов |

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

c2=a2+b2−2abcos⁡C,{displaystyle c^{2}=a^{2}+b^{2}-2abcos C,}

или:

cos⁡C=a2+b2−c22ab.{displaystyle cos C={frac {a^{2}+b^{2}-c^{2}}{2ab}}.}

Теорема тангенсов |

a−ba+b=tg⁡[12(A−B)]tg⁡[12(A+B)]{displaystyle {frac {a-b}{a+b}}={frac {mathop {operatorname {tg} } left[{tfrac {1}{2}}(A-B)right]}{mathop {operatorname {tg} } left[{tfrac {1}{2}}(A+B)right]}}}

Формула Эйлера |

Формула Эйлера утверждает, что для любого действительного числа x{displaystyle x} выполнено следующее равенство:

eix=cos⁡x+isin⁡x,{displaystyle e^{ix}=cos x+isin x,}

где e{displaystyle e} — основание натурального логарифма, i{displaystyle i} — мнимая единица.
Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:

cos⁡x=Re{eix}=eix+e−ix2,{displaystyle cos x=mathrm {Re} {e^{ix}}={e^{ix}+e^{-ix} over 2},}

sin⁡x=Im{eix}=eix−e−ix2i.{displaystyle sin x=mathrm {Im} {e^{ix}}={e^{ix}-e^{-ix} over 2i}.}

Вышеуказанные уравнения могут быть получены путём сложения или вычитания формул Эйлера:

eix=cos⁡x+isin⁡x,{displaystyle e^{ix}=cos x+isin x;,}

e−ix=cos⁡(−x)+isin⁡(−x)=cos⁡x−isin⁡x.{displaystyle e^{-ix}=cos(-x)+isin(-x)=cos x-isin x;.}

с последующим решением относительно синуса или косинуса.

Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:

cos⁡iy=e−y+ey2=ch⁡y,{displaystyle cos iy={e^{-y}+e^{y} over 2}=operatorname {ch} y,}

sin⁡iy=e−y−ey2i=−1iey−e−y2=ish⁡y.{displaystyle sin iy={e^{-y}-e^{y} over 2i}=-{1 over i}{e^{y}-e^{-y} over 2}=ioperatorname {sh} y.}

Комплексные экспоненты позволяют упростить тригонометрические расчеты, поскольку ими проще манипулировать, нежели синусоидальными компонентами. Один из подходов предусматривает преобразование синусоид в соответствующие экспоненциальные выражения. После упрощения результат выражения остается вещественным. Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением.

Решение простых тригонометрических уравнений |

• sin⁡x=a.{displaystyle sin x=a.}

Если |a|>1{displaystyle |a|>1} — вещественных решений нет.

Если |a|⩽1{displaystyle |a|leqslant 1} — решением является число вида x=(−1)narcsin⁡a+πn; n∈Z.{displaystyle x=(-1)^{n}arcsin a+pi n; nin mathbb {Z} .}

• cos⁡x=a.{displaystyle cos x=a.}

Если |a|>1{displaystyle |a|>1} — вещественных решений нет.

Если |a|⩽1{displaystyle |a|leqslant 1} — решением является число вида x=±arccos⁡a+2πn; n∈Z.{displaystyle x=pm arccos a+2pi n; nin mathbb {Z} .}

• tgx=a.{displaystyle operatorname {tg} ,x=a.}

Решением является число вида x=arctga+πn; n∈Z.{displaystyle x=operatorname {arctg} ,a+pi n; nin mathbb {Z} .}

• ctgx=a.{displaystyle operatorname {ctg} ,x=a.}

Решением является число вида x=arcctga+πn; n∈Z.{displaystyle x=operatorname {arcctg} ,a+pi n; nin mathbb {Z} .}

Сферическая тригонометрия |

Важным частным разделом тригонометрии, используемым в астрономии, геодезии, навигации и других отраслях, является сферическая тригонометрия, рассматривающая свойства углов между большими кругами на сфере и дуг этих больших кругов. Геометрия сферы существенно отличается от евклидовой планиметрии; так, сумма углов сферического треугольника, вообще говоря, отличается от 180°, треугольник может состоять из трёх прямых углов. В сферической тригонометрии длины сторон треугольника (дуги больших кругов сферы) выражаются посредством центральных углов, соответствующих этим дугам. Поэтому, например, сферическая теорема синусов выражается в виде

sin⁡asin⁡A=sin⁡bsin⁡B=sin⁡csin⁡C,{displaystyle {frac {sin a}{sin A}}={frac {sin b}{sin B}}={frac {sin c}{sin C}},}

и существуют две теоремы косинусов, двойственные друг другу.

См. также |

• 
  Гониометрия — раздел тригонометрии, где изучаются способы измерения углов, свойства тригонометрических функций и соотношения между ними.


• Решение треугольников


• Тригонометрические тождества


• Тригонометрические функции

Примечания |

Литература |

английская

• Boyer, Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — ISBN 0-471-54397-7.


• Christopher M. Linton (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy . Cambridge University Press.


• Weisstein, Eric W. «Trigonometric Addition Formulas». Wolfram MathWorld. Weiner.