Теорема о равнораспределении

Тепловое движение α-пептида. Сложное дрожащее движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого атома так и среднюю потенциальную энергию многих колебаний. Серые, красные и синие шары обозначают атомы углерода, кислорода и азота, соответственно; маленькие белые шарики представляют атомы водорода
Теорема о равнораспределении кинетической энергии по степеням свободы, закон равнораспределения, теорема о равнораспределении — связывает температуру системы с её средней энергией в классической статистической механике. В первоначальном виде теорема утверждала, что при тепловом равновесии энергия разделена одинаково между её различными формами, например, средняя кинетическая энергия поступательного движения молекулы должна равняться средней кинетической энергии её вращательного движения.
С помощью теоремы о равнораспределении можно делать количественные предсказания. Как и вириальная теорема, она даёт полные средние кинетические и потенциальные энергии для системы при данной температуре, из которых можно вычислить теплоёмкость системы. Однако теорема о равнораспределении также позволяет определить средние значения отдельных компонентов энергии, такие как кинетическая энергия одной частицы или потенциальная энергия отдельной пружины. В теореме утверждается, что каждая молекула одноатомного идеального газа, находящегося в термодинамическом равновесии (или в состоянии, близком к термодинамически равновесному), обладает средней кинетической энергией равной (3/2)kBT, где kB — постоянная Больцмана, T — температура. В общем случае её можно применять к любой классической системе, находящейся в состоянии теплового равновесия, независимо от того, насколько она сложна. Теорема о равнораспределении может использоваться для вывода уравнения состояния идеального газа и закона Дюлонга — Пти, для определения удельной теплоёмкости твёрдых тел. Её также используют в предсказании свойств звёзд, даже таких как белые карлики и нейтронные звезды, поскольку закон равнораспределения остаётся верен даже когда следует учитывать релятивистские эффекты.
Хотя теорема о равнораспределении делает очень точные предсказания при определённых условиях, она теряет применимость, когда квантовые эффекты начинают играть существенную роль. Равнораспределение действительно только тогда, когда тепловая энергия kBT намного больше, чем интервал между соседними квантовыми уровнями энергии, потому что в противном случае средние значения энергии и теплоёмкости, приходящиеся на некоторые степени свободы, меньше, чем величины, полученные с использованием теоремы о равнораспределении. Говорят, что степень свободы выморожена, если тепловая энергия намного меньше, чем этот интервал (это означает, что практически такую степень свободы при данных условиях можно не учитывать, при таком условии переход в возбужденные состояния по данной степени свободы практически невозможен). Например, теплоёмкость твёрдого тела уменьшается при низких температурах - поскольку различные типы движения становятся вымороженными - вместо того, чтобы остаться постоянной, как это должно было бы быть в соответствии с классической теоремой о равнораспределении. Такое уменьшение теплоёмкости было первым знаком физикам 19-го столетия, что классическая физика теряет применимость при низкой температуре, и должны быть сформулированы новые законы для объяснения реально наблюдаемого поведения теплоемкости в зависимости от температуры. Наряду с другим противоречием, несостоятельностью закона равнораспределения для описания электромагнитного излучения — также известного как ультрафиолетовая катастрофа — привели Макса Планка к идее, что свет излучается и поглощается квантами. Эта революционная гипотеза положила начало квантовой теории, давшей при дальнейшей разработке квантовую механики и квантовую теорию поля.
Содержание
1 Основная идея и простые примеры
1.1 Энергия поступательного движения частиц идеальных газов
1.2 Энергия вращательного движения
1.3 Потенциальная энергия и гармонические осцилляторы
1.4 Теплоёмкость твёрдых тел
1.5 Седиментация частиц
2 История
3 Общая формулировка теоремы о равнораспределении
3.1 Связь с вириальной теоремой
4 Применения
4.1 Уравнение состояния идеального газа
4.2 Двухатомные газы
4.3 Ультрарелятивистские идеальные газы
4.4 Неидеальные газы
4.5 Ангармонические осцилляторы
4.6 Броуновское движение
4.7 Физика звёзд
4.8 Звездообразование
5 Выводы
5.1 Кинетическая энергия и распределение Максвелла—Больцмана
5.2 Квадратичные энергии и статистическая сумма
5.3 Общие доказательства
5.3.1 Канонический ансамбль
5.3.2 Микроканонический ансамбль
6 Применимость
6.1 Требование эргодичности
6.2 Ограничения, накладываемые квантовой механикой
7 См. также
8 Примечания
9 Литература
10 Ссылки
Основная идея и простые примеры |
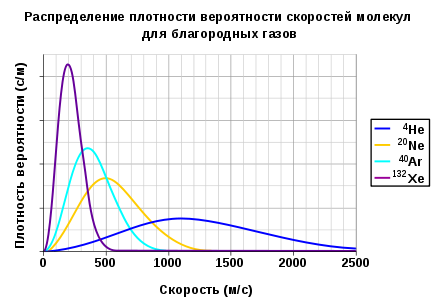
Распределение плотности вероятности скоростей молекул для четырёх благородных газов при температуре 298,15 К (25 °C). Показаны гелий (4He), неон (20Ne), аргон (40Ar) и ксенон (132Xe) (индекс обозначает их массовые числа). Функции распределения плотности вероятности имеют размерность вероятности, деленной на скорость, а поскольку вероятность — величина безразмерная, то результирующую размерность можно выразить в единицах секунда на метр.
Первоначально термин «равнораспределение» означал, что полная кинетическая энергия системы разделена одинаково среди всех её независимых частей в среднем, как только система достигла теплового равновесия. Теорема о равнораспределении также даёт количественные предсказания для этих энергий. Например, она предсказывает, что каждый атом благородного газа, находящегося в тепловом равновесии при температуре T, обладает средней кинетической энергией поступательного движения равной (3/2)kBT. Как следствие, более тяжёлые атомы ксенона обладают более низкой средней скоростью, чем лёгкие атомы гелия при той же самой температуре. Рисунок показывает распределение Максвелла для скоростей атомов четырёх газов.
В этом примере важно отметить, что кинетическая энергия является квадратичной функцией скорости. Теорема о равнораспределении утверждает, что при тепловом равновесии, любая степень свободы (компоненты векторов положения или скорость частицы)[1], которая появляется только как квадратичная функция в энергии, обладает средней энергией равной ½kBT и поэтому вносит вклад ½kB в теплоёмкость системы. У этого утверждения существует много практических приложений.
Энергия поступательного движения частиц идеальных газов |
Кинетическая энергия частицы газа с массой m и обладающая скоростью v задаётся в виде
- Hkin=12m|v|2=12m(vx2+vy2+vz2),{displaystyle H^{mathrm {kin} }={tfrac {1}{2}}m|mathbf {v} |^{2}={tfrac {1}{2}}mleft(v_{x}^{2}+v_{y}^{2}+v_{z}^{2}right),}
где vx, vy и vz — декартовы компоненты вектора скорости v. Здесь символ H обозначает функцию Гамильтона системы и используется как символ энергии в гамильтоновом формализме. Он играет центральную роль в большинстве обобщений закона равнораспределения.
Поскольку кинетическая энергия является квадратичной функцией компонент скорости, из закона равнораспределения следует, что каждая из этих компонент вносит одинаковый вклад ½kBT в среднюю кинетическую энергию газа находящегося в тепловом равновесии. Отсюда следует, что средняя кинетическая энергия частицы равна (3/2)kBT, как в примере для благородных газов сверху.
В общем случае, полная энергия идеального газа состоит из (поступательной) кинетической энергии отдельных частиц, в соответствии с предположением, что частицы не имеют никаких внутренних степеней свободы и перемещаются независимо от друг друга. Равнораспределение означает, что средняя полная энергия идеального газа из N частиц равна (3/2)N kBT.
Отсюда следует, что теплоёмкость газа составляет (3/2)N kB и, в частности, теплоёмкость одного моля газа таких частиц равна (3/2)NAkB=(3/2)R, где NA — число Авогадро и R — газовая постоянная. Поскольку R ≈ 2 кал/(моль·К), закон равнораспределения предсказывает что молярная теплоёмкость идеального газа приблизительно равна 3 кал/(моль·К). Это предсказание проверено экспериментально.[2]
Средняя кинетическая энергия позволяет оценить корень квадратный из среднего квадрата скорости vrms частиц в газе:
- vrms=⟨v2⟩=3kBTm=3RTM,{displaystyle v_{mathrm {rms} }={sqrt {langle v^{2}rangle }}={sqrt {frac {3k_{B}T}{m}}}={sqrt {frac {3RT}{M}}},}
где M = NAm — молярная масса газа. Этот результат полезен для многих практических приложений, таких как закон Грэхема для эффузии, который используется в методе обогащения урана[3]
Энергия вращательного движения |
Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I1, I2 и I3. Вращательная энергия такой молекулы задана выражением
- Hrot=12(I1ω12+I2ω22+I3ω32),{displaystyle H^{mathrm {rot} }={frac {1}{2}}(I_{1}omega _{1}^{2}+I_{2}omega _{2}^{2}+I_{3}omega _{3}^{2}),}
где ω1, ω2, и ω3 — главные компоненты угловой скорости. Точно по тем же самым рассуждениям как и в случае поступательного движения равнораспределение подразумевает, что при тепловом равновесии средняя вращательная энергия каждой частицы: (3/2)kBT. Аналогично, теорема о равнораспределении позволяет вычислить среднюю (более точно, корень квадратный из среднего квадрата) угловую скорость молекул.[4]
Потенциальная энергия и гармонические осцилляторы |
Равнораспределение применимо не только к кинетической энергии, но и к потенциальной энергии. Важные примеры включают гармонические осцилляторы такие как пружина, которая обладает квадратичной по координатам потенциальной энергией
- Hpot=12aq2,{displaystyle H^{mathrm {pot} }={tfrac {1}{2}}aq^{2},}
где постоянная a описывает жёсткость пружины и q — отклонение от равновесного положения. Если такая одномерная система имеет массу m, тогда её кинетическая энергия Hkin: ½mv² = p²/2m, где v и p = mv обозначают скорость и импульс осциллятора. Суммируя эти вклады получим полную энергию системы[5]
- H=Hkin+Hpot=p22m+12aq2.{displaystyle H=H^{mathrm {kin} }+H^{mathrm {pot} }={frac {p^{2}}{2m}}+{frac {1}{2}}aq^{2}.}
Равнораспределение подразумевает, что при тепловом равновесии осциллятор обладает средней энергией, которая равна
- ⟨H⟩=⟨Hkin⟩+⟨Hpot⟩=12kBT+12kBT=kBT,{displaystyle langle Hrangle =langle H^{mathrm {kin} }rangle +langle H^{mathrm {pot} }rangle ={tfrac {1}{2}}k_{B}T+{tfrac {1}{2}}k_{B}T=k_{B}T,}
где угольные скобки ⟨…⟩{displaystyle leftlangle ldots rightrangle }
Этот результат остаётся верен для любого типа гармонического осциллятора, таких как маятник, колеблющаяся молекула или пассивный электрический генератор. Системы таких осцилляторов возникают во многих случаях. По закону равнораспределения, каждый такой осциллятор обладает средней полной энергией kBT и следовательно даёт вклад kB в теплоёмкость системы. Этот вывод можно использовать для вывода формулы для теплового шума[7] и закона Дюлонга — Пти для удельной теплоёмкости твёрдых тел. Последнее сыграло важную роль в истории теоремы о равнораспределении.

Теплоёмкость твёрдых тел |
Закон равнораспределения применяется для определения удельной теплоёмкости кристаллических тел. Поскольку каждый атом из такого тела может колебаться в трёх независимых направлениях, то кристалл можно рассматривать как систему 3N независимых гармонических осцилляторов, где N обозначает число атомов в решётке. Каждый гармонический осциллятор обладает средней энергией kBT, поэтому средняя полная энергия тела равна 3NkBT, а его удельная теплоёмкость 3NkB.
Если взять за N — число Авогадро (NA), то, используя соотношение R = NAkB между газовой постоянной (R) и постоянной Больцмана (kB), получим выражение для закона Дюлонга — Пти, который описывает молярную теплоёмкость твёрдых тел. Он гласит, что удельная теплоёмкость одного моля атомов кристаллической решётки составляет 3R ≈ 6 кал/(моль·К).
Следует отметить, что этот закон неверен при низких температурах, где важно принять во внимание квантовые эффекты. Он также вступает в противоречие с экспериментально подтверждённым третьим началом термодинамики, согласно которому удельная теплоёмкость любого вещества стремится к нулю при стремлении температуры к абсолютному нулю.[7] Более точные теории, которые принимают во внимание квантовые эффекты, были разработаны Альбертом Эйнштейном (1907 год) и Петером Дебаем (1911 год).[8]
Многие физические системы можно смоделировать в виде системы связанных гармонических осцилляторов. Движения таких осцилляторов можно разложить на нормальные моды, которые можно представить как вибрационные моды струны фортепьяно или резонансы трубы органа. С другой стороны, теорема о равнораспределении становится неприменимой для таких систем из-за отсутствия обмена энергии между нормальными модами. В предельном случае моды независимы и, таким образом, их энергии сохраняются независимо. Это означает, что смешивание энергий, формально называемое эргодичностью, важно для выполнения закона равнораспределения.
Седиментация частиц |
Потенциальная энергия не всегда является квадратичной функцией координат, но теорема о равнораспределении утверждает, что если степень свободы x входит с множителем xs (для фиксированной постоянной s) в полную энергию, то при тепловом равновесии средняя энергия этой части равна kBT/s.
Это обобщение используется при рассмотрении седиментации частиц под действием гравитации.[9] Например, взвесь, иногда заметная в пиве, может быть вызвана кусочками белков, которые рассеивают свет.[10] В течение долгого времени, эти кусочки скапливаются на дне под действием силы тяжести, приводя к более сильному рассеянию света около основания бутылки, чем у её вершины. Однако, благодаря диффузии работающей в противоположном направлении, частицы движутся вверх к вершине бутылки. Как только равновесие достигнуто, теорема о равнораспределении может использоваться, чтобы определить среднее положение определённого кусочка плавучей массы mb. Для бесконечно высокой бутылки пива гравитационная потенциальная энергия задана в виде
- Hgrav=mbgz,{displaystyle H^{mathrm {grav} }=m_{b}gz,,}
где z — положение белкового кусочка в бутылке по высоте и g — ускорение вызванное гравитацией. Поскольку s=1, то средняя потенциальная энергия белкового кусочка равна kBT. Если масса белкового кусочка составляет около 10 МДа (грубо это размер вируса), то при равновесии возникнет взвесь со средней высотой около 2 см. Процесс седиментации к равновесному положению описывается уравнением Масона — Вивера.[11]
История |
- В этой статье используются отличные от СИ единицы измерения кал/(моль·К) для удельной теплоёмкости из-за точности десятичной записи.
Для преобразования в единицы СИ Дж/(моль·К), эти значения нужно домножить на 4.2 Дж/кал.
Равнораспределение кинетической энергии по степеням свободы предложил в 1843 году (правильнее говорить о 1845 годе) Джон Джеймс Уотерстон.[12][13][14][15][16] В 1859, Джеймс Клерк Максвелл утверждал, что кинетическая энергия при высокой температуре газа одинаково разделена между энергией поступательного движения и вращательной энергией.[17] В 1876 году, Людвиг Больцман показал, что средняя энергия разделена одинаково между всех независимых компонент движения в системе.[18][19] Больцман применил закон равнораспредедления, чтобы теоретически объяснить эмпирический закон Дюлонга — Пти для теплоёмкости твёрдых тел.

Идеализированный график теплоёмкости двухатомного газа в зависимости от температуры. Значение (7/2)R согласуется с предсказанной из закона равнораспределения теплоёмкостью для высоких температур (где R газовая постоянная), но уменьшается до (5/2)R и затем до (3/2)R при более низких температурах, поскольку колебательные и вращательные степени свободы вымораживаются. Нарушение закона равнораспределения привело к парадоксу, который был разрешён только в квантовой механике. Для большинства молекул переходная температура Trot много меньше комнатной температуры, в то время как Tvib может быть в десять раз больше. (Типичный пример: монооксид углерода, CO, для которого Trot ≈ 2.8 К, а Tvib ≈ 3103 К.) Для молекул с длинными или слабыми связями между атомами, Tvib может быть близка к комнатной температуре (около 300 КK); например, Tvib ≈ 308 К для газа йода, I2.[20]
История теоремы о равнораспределении переплетена с исследованиями теплоёмкости, которые были проведены в 19-м столетии. В 1819 году французские физики Пьер Дюлонг и Алексис Пти обнаружили, что удельные молярные теплоёмкости для твёрдых тел практически равны при комнатной температуре, и составляют приблизительно 6 кал/(моль·К).[21] Их закон использовался многие годы для измерения атомных весов.[8] Однако последующие исследования Джеймса Дьюара и Генриха Вебера показали, что закон Дюлонга-Пти выполняется только при больших температурах,[22][23][24] а при низких температурах или для очень твёрдых кристаллов, таких как алмаз, теплоёмкость меньше.[25][26][27]
Экспериментальные значения теплоёмкости газов также поставили вопросы о правильности теоремы о равнораспределении. Теорема предсказывает, что молярная удельная теплоёмкость одноатомных газов должна быть примерно 3 кал/(моль·К), а для двухатомных газов приблизительно 7 кал/(моль·К). Эксперименты подтвердили первое предсказание,[2] но для двухатомных газов эксперимент показал, что удельная молярная теплоёмкость составляет только 5 кал/(моль·К),[28] и падает до 3 кал/(моль·К) при очень низких температурах.[29] Максвелл заметил в 1875, что расхождение между экспериментом и законом равнораспределения даже хуже, если брать эти значения;[30] поскольку атомы имеют внутреннюю структуру, то тепловая энергия должна пойти на движение этих внутренних частей, приводя к предсказаниям для удельных молярных теплоёмкостей одноатомных и двухатомных газов много больших чем 3 кал/(моль·К) и 7 кал/(моль·К), соответственно.
Третье разногласие связано с теплоёмкостью металлов.[31] Согласно классической модели Друде, электроны в металле ведут себя как идеальный газ и соответственно должны давать вклад (3/2)Ne kB, где Ne — число электронов, в теплоёмкость металла по теореме о равнораспределении. Экспериментально, однако, вклад электронов в теплоёмкость невелик: молярные теплоёмкости различных проводников и диэлектриков практически совпадают.[31] (См. также раздел «Ограничения, накладываемые квантовой механикой»).
Были предложены несколько объяснений неточности теоремы о равнораспределении при определении теплоёмкостей. Больцман защищал доказательство своей теоремы как правильное, но предположил, что газы могут не быть в тепловом равновесии из-за их взаимодействия с эфиром.[32]Лорд Кельвин предположил, что вывод теоремы о равнораспределении должен быть неверен, поскольку её выводы расходятся с экспериментом, но не смог указать ошибку.[33]Лорд Рэлей вместо этого выдвинул более радикальную гипотезу, заключающуюся в том что и теорема о равнораспределении и экспериментальное предположение о тепловом равновесии верны, но чтобы согласовать их, он высказался о потребности нового принципа, который обеспечит побег от разрушительной простоты теоремы о равнораспределении.[34]Альберт Эйнштейн показал путь для разрешения этого противоречия, когда в 1907 году показал, что эти аномалии в теплоёмкости возникают из-за квантовых эффектов, в частности квантования энергии упругих колебаний твёрдого тела.[35][36][37][38][39] Эйнштейн использовал неточность закона равнораспределения как довод в пользу потребности новой квантовой теории вещества.[8] Эксперименты Нернста в 1910 году по измерению теплоёмкости при низких температурах[40] подтвердили теорию Эйнштейна и привели к широкой поддержке квантовой теории среди физиков.[41]
Общая формулировка теоремы о равнораспределении |
Наиболее общая формулировка теоремы о равнораспределении[4][6][9] гласит, что при определённых условиях (смотрите ниже), для физической системы с гамильтонианом H и степенями свободы xn, выполняется следующее соотношение для любых индексов m и n:
- ⟨xm∂H∂xn⟩=δmnkBT.{displaystyle {Bigl langle }x_{m}{frac {partial H}{partial x_{n}}}{Bigr rangle }=delta _{mn}k_{B}T.}
Здесь δmn — символ Кронекера, который равен единице если m=n и нулю в других случаях. Угловые скобки обозначают усреднение ⟨…⟩{displaystyle leftlangle ldots rightrangle }
Общая формулировка теоремы верна как в случае микроканонического ансамбля,[6] когда полная энергии системы постоянна, так и в случае канонического ансамбля,[4][42] когда система связана с тепловым резервуаром, с которым она может обмениваться энергией. Вывод общей формулы приведён ниже.
Общая формула эквивалентна следующим выражениям:
⟨xn∂H∂xn⟩=kBT{displaystyle {Bigl langle }x_{n}{frac {partial H}{partial x_{n}}}{Bigr rangle }=k_{B}T}для всех n.
⟨xm∂H∂xn⟩=0{displaystyle {Bigl langle }x_{m}{frac {partial H}{partial x_{n}}}{Bigr rangle }=0}для всех m≠n.
Если степень свободы xn появляется только в виде квадратичного слагаемого anxn² в гамильтониане H, то первая формула утверждает, что
- kBT=⟨xn∂H∂xn⟩=2⟨anxn2⟩,{displaystyle k_{B}T={Bigl langle }x_{n}{frac {partial H}{partial x_{n}}}{Bigr rangle }=2langle a_{n}x_{n}^{2}rangle ,}
в два раза больше вклада этой степени свободы в среднюю энергию ⟨H⟩{displaystyle langle Hrangle }
Степени свободы xn — координаты в фазовом пространстве системы, и поэтому они обычно разделяются на обобщённые координаты qk и обобщённые импульсы pk, где pk — сопряжённый импульс к qk. В этом случае формула 1 означает, что для всех k
- ⟨pk∂H∂pk⟩=⟨qk∂H∂qk⟩=kBT.{displaystyle {Bigl langle }p_{k}{frac {partial H}{partial p_{k}}}{Bigr rangle }={Bigl langle }q_{k}{frac {partial H}{partial q_{k}}}{Bigr rangle }=k_{B}T.}
Используя уравнения гамильтоновой механики,[5] эти формулы можно также переписать в виде
- ⟨pkdqkdt⟩=−⟨qkdpkdt⟩=kBT.{displaystyle {Bigl langle }p_{k}{frac {dq_{k}}{dt}}{Bigr rangle }=-{Bigl langle }q_{k}{frac {dp_{k}}{dt}}{Bigr rangle }=k_{B}T.}
Формула 2 утверждает, что средние
⟨qj∂H∂qk⟩,⟨qj∂H∂pk⟩,⟨pj∂H∂pk⟩,⟨pj∂H∂qk⟩,⟨qk∂H∂pk⟩,{displaystyle {Bigl langle }q_{j}{frac {partial H}{partial q_{k}}}{Bigr rangle },quad {Bigl langle }q_{j}{frac {partial H}{partial p_{k}}}{Bigr rangle },quad {Bigl langle }p_{j}{frac {partial H}{partial p_{k}}}{Bigr rangle },quad {Bigl langle }p_{j}{frac {partial H}{partial q_{k}}}{Bigr rangle },quad {Bigl langle }q_{k}{frac {partial H}{partial p_{k}}}{Bigr rangle },}и ⟨pk∂H∂qk⟩{displaystyle {Bigl langle }p_{k}{frac {partial H}{partial q_{k}}}{Bigr rangle }}
равны нулю для j≠k.
Связь с вириальной теоремой |
Общая теорема о равнораспределении является обобщением теоремы о вириале (предложена в 1870[43]) и гласит
- ⟨∑kqk∂H∂qk⟩=⟨∑kpk∂H∂pk⟩=⟨∑kpkdqkdt⟩=−⟨∑kqkdpkdt⟩,{displaystyle {Bigl langle }sum _{k}q_{k}{frac {partial H}{partial q_{k}}}{Bigr rangle }={Bigl langle }sum _{k}p_{k}{frac {partial H}{partial p_{k}}}{Bigr rangle }={Bigl langle }sum _{k}p_{k}{frac {dq_{k}}{dt}}{Bigr rangle }=-{Bigl langle }sum _{k}q_{k}{frac {dp_{k}}{dt}}{Bigr rangle },}
где t обозначает время.[5] Два ключевых различия между ними заключаются в том, что вириальная теорема связывает «суммированные», а не «индивидуальные» средние друг с другом, и первая не связывает их с температурой «T». Другое различие — то, что традиционные доказательства вириальной теоремы используют усреднение в течение длительного периода времени, тогда как теорема о равнораспределении также использует усреднение по фазовому пространству.
Применения |
Уравнение состояния идеального газа |
Теорема о равнораспределении используется для вывода уравнения состояния идеального газа из классической механики.[4]. Формула для средней кинетической энергии на одну частицу, принимая во внимание только три поступательных степени свободы, запишется в виде
- ⟨Hkin⟩=12m⟨px2+py2+pz2⟩=12(⟨px∂Hkin∂px⟩+⟨py∂Hkin∂py⟩+⟨pz∂Hkin∂pz⟩)=32kBT{displaystyle {begin{aligned}langle H^{mathrm {kin} }rangle &={frac {1}{2m}}langle p_{x}^{2}+p_{y}^{2}+p_{z}^{2}rangle \&={frac {1}{2}}{biggl (}{Bigl langle }p_{x}{frac {partial H^{mathrm {kin} }}{partial p_{x}}}{Bigr rangle }+{Bigl langle }p_{y}{frac {partial H^{mathrm {kin} }}{partial p_{y}}}{Bigr rangle }+{Bigl langle }p_{z}{frac {partial H^{mathrm {kin} }}{partial p_{z}}}{Bigr rangle }{biggr )}={frac {3}{2}}k_{B}Tend{aligned}}}
Если q = (qx, qy, qz) и p = (px, py, pz) обозначают координаты и импульс частицы в газе, а F — сила, действующая на эту частицу, тогда
- ⟨q⋅F⟩=⟨qxdpxdt⟩+⟨qydpydt⟩+⟨qzdpzdt⟩=−⟨qx∂H∂qx⟩−⟨qy∂H∂qy⟩−⟨qz∂H∂qz⟩=−3kBT,{displaystyle {begin{aligned}langle mathbf {q} cdot mathbf {F} rangle &={Bigl langle }q_{x}{frac {dp_{x}}{dt}}{Bigr rangle }+{Bigl langle }q_{y}{frac {dp_{y}}{dt}}{Bigr rangle }+{Bigl langle }q_{z}{frac {dp_{z}}{dt}}{Bigr rangle }\&=-{Bigl langle }q_{x}{frac {partial H}{partial q_{x}}}{Bigr rangle }-{Bigl langle }q_{y}{frac {partial H}{partial q_{y}}}{Bigr rangle }-{Bigl langle }q_{z}{frac {partial H}{partial q_{z}}}{Bigr rangle }=-3k_{B}T,end{aligned}}}
где первое равенство представляет собой второй закон Ньютона, а вторая строчка использует уравнения Гамильтона и равнораспределение. Суммирование по системе из N частиц приводит к выражению
- 3NkBT=−⟨∑k=1Nqk⋅Fk⟩.{displaystyle 3Nk_{B}T=-{biggl langle }sum _{k=1}^{N}mathbf {q} _{k}cdot mathbf {F} _{k}{biggr rangle }.}
Используя третий закон Ньютона и предположение об идеальности газа, получим полную силу в системе — силу, которая действует со стороны стенок контейнера на систему, и эта сила задаётся давлением P газа. Следовательно
- −⟨∑k=1Nqk⋅Fk⟩=P∮surfaceq⋅dS,{displaystyle -{biggl langle }sum _{k=1}^{N}mathbf {q} _{k}cdot mathbf {F} _{k}{biggr rangle }=Point _{mathrm {surface} }mathbf {q} cdot mathbf {dS} ,}
где dS — бесконечно малый элемент площади стенок контейнера. Поскольку дивергенция радиус-вектора q равняется
- ∇⋅q=∂qx∂qx+∂qy∂qy+∂qz∂qz=3,{displaystyle {boldsymbol {nabla }}cdot mathbf {q} ={frac {partial q_{x}}{partial q_{x}}}+{frac {partial q_{y}}{partial q_{y}}}+{frac {partial q_{z}}{partial q_{z}}}=3,}
то из теоремы о дивергенции получаем
- P∮surfaceq⋅dS=P∫volume(∇⋅q)dV=3PV,{displaystyle Point _{mathrm {surface} }mathbf {q} cdot mathbf {dS} =Pint _{mathrm {volume} }left({boldsymbol {nabla }}cdot mathbf {q} right)dV=3PV,}
где dV — бесконечно малый объём внутри контейнера, V — его полный объём.
Собирая уравнения вместе, получаем
- 3NkBT=−⟨∑k=1Nqk⋅Fk⟩=3PV,{displaystyle 3Nk_{B}T=-{biggl langle }sum _{k=1}^{N}mathbf {q} _{k}cdot mathbf {F} _{k}{biggr rangle }=3PV,}
которое приводит к уравнению состояния для идеального газа для N частиц:
- PV=NkBT=nRT,{displaystyle PV=Nk_{B}T=nRT,}
где n=N/NA — число молей газа и R=NAkB — газовая постоянная.[44]
Двухатомные газы |
Двухатомный газ можно представить как соединённые между собой посредством пружины с жёсткостью a, две массы m1 и m2.[20] Классическая энергия этой системы записывается в виде суммы кинетических энергий движения отдельных масс и потенциальной энергии деформации пружины:
- H=|p1|22m1+|p2|22m2+12aq2,{displaystyle H={frac {left|mathbf {p} _{1}right|^{2}}{2m_{1}}}+{frac {left|mathbf {p} _{2}right|^{2}}{2m_{2}}}+{frac {1}{2}}aq^{2},}
где p1 и p2 — импульсы двух атомов, q — отклонение от положения равновесия. Каждая степень свободы является квадратичной функцией, и поэтому должна давать вклад равный ½kBT к полной средней энергии и ½kB к удельной теплоёмкости. Таким образом, удельная теплоёмкость газа из N двухатомных молекул должна равняться 7N · ½kB: импульсы p1 и p2 дают каждый по три степени свободы и отклонение q добавляет седьмую. Отсюда следует, что удельная теплоёмкость одного моля газа двухатомных молекул без каких-либо отличных от упомянутых выше степеней свободы должна составить (7/2)NAkB=(7/2)R и, таким образом, предсказанная молярная удельная теплоёмкость составит 7 кал/(моль·К). В то же время, как показали измерения, молярная удельная теплоёмкость газа двухатомных молекул равняется 5 кал/(моль·К)[28] и уменьшается до 3 кал/(моль·К) при очень низких температурах.[29] Это расхождение между предсказанным значением по закону равнораспределения и экспериментом нельзя объяснить, используя более сложную структуру молекулы, поскольку с добавлением степеней свободы увеличивается и предсказанное значение теплоёмкости.[30] Это разногласие было одним из ключевых, которые требовали более правильных, а именно квантовых представлений о структуре материи.

Совмещённое рентгеновское и оптическое изображения крабовидной туманности. В центре этой туманности находится быстро вращающаяся нейтронная звезда, которая в полтора раза тяжелее нашего Солнца, но только 25 км в диаметре. Теорема о равнораспределении оказывается полезной для изучения свойств таких звёзд
Ультрарелятивистские идеальные газы |
Закон равнораспределения использовался выше, чтобы получить классическое уравнение состояния идеального газа из ньютоновской механики. Однако релятивистские эффекты становятся доминирующими в некоторых системах, таких как белые карлики и нейтронные звезды,[6] и уравнение состояния идеального газа нужно изменить. Теорема о равнораспределении даёт удобный способ получить соответствующие законы для ультрарелятивистского идеального газа.[4] В этом случае, кинетическая энергия отдельной частицы задана формулой
- Hkin≈cp=cpx2+py2+pz2.{displaystyle H^{mathrm {kin} }approx cp=c{sqrt {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}}.}
Дифференцируя H по px компоненте импульса, получим
- px∂Hkin∂px=cpx2px2+py2+pz2{displaystyle p_{x}{frac {partial H^{mathrm {kin} }}{partial p_{x}}}=c{frac {p_{x}^{2}}{sqrt {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}}}}
и аналогично для py и pz компонент. Складывая три компоненты вместе прийдём к выражению для средней кинетической энергии
- ⟨Hkin⟩=⟨cpx2+py2+pz2px2+py2+pz2⟩=⟨px∂Hkin∂px⟩+⟨py∂Hkin∂py⟩+⟨pz∂Hkin∂pz⟩=3kBT{displaystyle {begin{aligned}langle H^{mathrm {kin} }rangle &={biggl langle }c{frac {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}{sqrt {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}}}{biggr rangle }\&={Bigl langle }p_{x}{frac {partial H^{mathrm {kin} }}{partial p_{x}}}{Bigr rangle }+{Bigl langle }p_{y}{frac {partial H^{mathrm {kin} }}{partial p_{y}}}{Bigr rangle }+{Bigl langle }p_{z}{frac {partial H^{mathrm {kin} }}{partial p_{z}}}{Bigr rangle }\&=3k_{B}Tend{aligned}}}
где последнее равенство следует из равнораспределения. Таким образом, средняя полная энергия ультрарелятивистского газа в два раза больше полной энергии газа в нерелятивистском случае: для N частиц, получим 3 N kBT.
Неидеальные газы |
В идеальном газе частицы взаимодействуют только через соударения. Закон равнораспределения можно использовать для получения выражения для давления и энергии «неидеальных газов», в которых частицы взаимодействуют друг с другом посредством консервативных сил. Потенциал взаимодействия U(r) этих частиц зависит только от расстояния r между частицами.[4] Эта ситуация описывается в модели одной частицы, где остальные частицы в газе образуют сферически-симметричное распределение. Удобно ввести радиальную функцию распределения g(r), такую что плотность вероятности найти частицу на расстоянии r от данной равна 4πr²ρ g(r), где ρ=N/V — средняя плотность газа.[45] Отсюда следует, что средняя потенциальная энергия взаимодействия частицы с её окружением равна
- ⟨hpot⟩=∫0∞4πr2ρU(r)g(r)dr.{displaystyle langle h^{mathrm {pot} }rangle =int _{0}^{infty }4pi r^{2}rho U(r)g(r),dr.}
Полная средняя потенциальная энергия газа равна ⟨Hpot⟩=12N⟨hpot⟩{displaystyle langle H^{pot}rangle ={tfrac {1}{2}}Nlangle h^{mathrm {pot} }rangle }
После суммирования потенциальной и кинетической энергии и применения равнораспределения получим энергетическое уравнение
- H=⟨Hkin⟩+⟨Hpot⟩=32NkBT+2πNρ∫0∞r2U(r)g(r)dr.{displaystyle H=langle H^{mathrm {kin} }rangle +langle H^{mathrm {pot} }rangle ={frac {3}{2}}Nk_{B}T+2pi Nrho int _{0}^{infty }r^{2}U(r)g(r),dr.}
Похожие рассуждения,[4] приводят к уравнению для давления
- 3NkBT=3PV+2πNρ∫0∞r3U′(r)g(r)dr.{displaystyle 3Nk_{B}T=3PV+2pi Nrho int _{0}^{infty }r^{3}U'(r)g(r),dr.}
Ангармонические осцилляторы |
Для ангармонического осциллятора (в противоположность простому гармоническому осциллятору) потенциальная энергия не является квадратичной функцией смещения q (обобщённая координата, которая показывает отклонение от положения равновесия). Такие осцилляторы позволяют более широко взглянуть на закон равнораспределения.[46][47] в качестве простого примера рассмотрим функции потенциальной энергии вида
- Hpot=Cqs,{displaystyle H^{mathrm {pot} }=Cq^{s},}
где C и s произвольные реальные постоянные. В этом случае закон равнораспределения приводит к выыражению
- kBT=⟨q∂Hpot∂q⟩=⟨q⋅sCqs−1⟩=⟨sCqs⟩=s⟨Hpot⟩.{displaystyle k_{B}T={Bigl langle }q{frac {partial H^{mathrm {pot} }}{partial q}}{Bigr rangle }=langle qcdot sCq^{s-1}rangle =langle sCq^{s}rangle =slangle H^{mathrm {pot} }rangle .}
Таким образом, средняя потенциальная энергия равна kBT/s, а не kBT/2 как для квадратичного потенциала гармонического осциллятора (где s=2).
Более обще, типичная функция энергии одномерной системы представима в виде разложения Тейлора по q:
- Hpot=∑n=2∞Cnqn{displaystyle H^{mathrm {pot} }=sum _{n=2}^{infty }C_{n}q^{n}}
для неотрицательных целых чисел n. Слагаемое с n=1 отсутствует, поскольку в точке равновесия отсутствует результирующая сила и первая производная энергии обращается в ноль. Слагаемое с n=0 нужно включить, поскольку потенциальная энергия в точке равновесия может быть выбрана произвольным образом (ноль для простоты). В этом случае из равнораспределения следует что[46]
- kBT=⟨q∂Hpot∂q⟩=∑n=2∞⟨q⋅nCnqn−1⟩=∑n=2∞nCn⟨qn⟩.{displaystyle k_{B}T={Bigl langle }q{frac {partial H^{mathrm {pot} }}{partial q}}{Bigr rangle }=sum _{n=2}^{infty }langle qcdot nC_{n}q^{n-1}rangle =sum _{n=2}^{infty }nC_{n}langle q^{n}rangle .}
В противоположность с другими примерами приведёнными здесь, закон равнораспределения
- ⟨Hpot⟩=12kBT−∑n=3∞(n−22)Cn⟨qn⟩{displaystyle langle H^{mathrm {pot} }rangle ={frac {1}{2}}k_{B}T-sum _{n=3}^{infty }left({frac {n-2}{2}}right)C_{n}langle q^{n}rangle }
для средней потенциальной энергии не может быть записан в терминах известных постоянных.
Броуновское движение |

Типичное броуновское движение частицы в трёх измерениях
Закон равнораспределения используют для вывода среднеквадратичного отклонения броуновской частицы, используя уравнение Ланжевена.[4] Согласно этому уравнению движение частицы с массой m и скоростью v управляется вторым законом Ньютона
- dvdt=1mF=−vτ+1mFrnd,{displaystyle {frac {dmathbf {v} }{dt}}={frac {1}{m}}mathbf {F} =-{frac {mathbf {v} }{tau }}+{frac {1}{m}}mathbf {F} ^{mathrm {rnd} },}
где Frnd — случайная сила, которая описывает случайные соударения частицы с окружающими молекулами, и где постоянная времени τ отражает существование силы трения которая направлена в противоположную движению сторону. Сила трения часто записывается в виде пропорциональном скорости частицы Fdrag = — γv, и тогда постоянная времени τ равна m/γ.
Скалярное произведение этого уравнения и вектора местоположения частицы r после усреднения (по времени) приводит к уравнению
- ⟨r⋅dvdt⟩+1τ⟨r⋅v⟩=0{displaystyle {Bigl langle }mathbf {r} cdot {frac {dmathbf {v} }{dt}}{Bigr rangle }+{frac {1}{tau }}langle mathbf {r} cdot mathbf {v} rangle =0}
для броуновского движения (поскольку случайная сила Frnd некоррелирована с вектором r). Используя математические соотношения
- ddt(r⋅r)=ddt(r2)=2(r⋅v){displaystyle {frac {d}{dt}}left(mathbf {r} cdot mathbf {r} right)={frac {d}{dt}}left(r^{2}right)=2left(mathbf {r} cdot mathbf {v} right)}
и
- ddt(r⋅v)=v2+r⋅dvdt,{displaystyle {frac {d}{dt}}left(mathbf {r} cdot mathbf {v} right)=v^{2}+mathbf {r} cdot {frac {dmathbf {v} }{dt}},}
основное уравнение для броуновского движения можно записать в виде
- d2dt2⟨r2⟩+1τddt⟨r2⟩=2⟨v2⟩=6mkBT,{displaystyle {frac {d^{2}}{dt^{2}}}langle r^{2}rangle +{frac {1}{tau }}{frac {d}{dt}}langle r^{2}rangle =2langle v^{2}rangle ={frac {6}{m}}k_{B}T,}
где последнее равенство следует из закона равнораспределения для кинетической энергии поступательного движения:
- ⟨Hkin⟩=⟨p22m⟩=⟨12mv2⟩=32kBT.{displaystyle langle H^{mathrm {kin} }rangle ={Bigl langle }{frac {p^{2}}{2m}}{Bigr rangle }=langle {tfrac {1}{2}}mv^{2}rangle ={tfrac {3}{2}}k_{B}T.}
Тогда дифференциальное уравнение для ⟨r2⟩{displaystyle langle r^{2}rangle }
- ⟨r2⟩=6kBTτ2m(e−t/τ−1+tτ).{displaystyle langle r^{2}rangle ={frac {6k_{B}Ttau ^{2}}{m}}left(e^{-t/tau }-1+{frac {t}{tau }}right).}
Если время мало по сравнению с постоянной времени (t << τ), то частицу можно рассматривать как свободно движущуюся, и используя разложение Тейлора для экспоненциальной функции, поскольку квадрат смещения растёт приблизительно квадратично получим
- ⟨r2⟩≈3kBTmt2=⟨v2⟩t2.{displaystyle langle r^{2}rangle approx {frac {3k_{B}T}{m}}t^{2}=langle v^{2}rangle t^{2}.}
При временах много больших постоянной времени (t >> τ) экспоненциальное слагаемое и константа пренебрежимо малы и квадрат смещения растёт линейно:
- ⟨r2⟩≈6kBTτmt=6γkBTt.{displaystyle langle r^{2}rangle approx {frac {6k_{B}Ttau }{m}}t=6gamma k_{B}Tt.}
Это выражение описывает диффузию частицы во времени. Аналогичное уравнение для вращательной диффузии жёсткой молекулы выводится аналогичным методом.

Теорема о равнораспределении даёт правильную оценку для температуры внутри ядра Солнца
Физика звёзд |
Теорема о равнораспределении и вириальная теорема давно используется в астрофизике.[48] Например, вириальную теорему используют для оценки температур звёзд или предела Чандрасекара для массы белых карликов.[49][50]
Средняя температура звезды оценивается из теоремы о равнораспределении.[51] Поскольку большинство звёзд сферически симметричны, то полная гравитационная потенциальная энергия оценивается интегралом
- Htotgrav=−∫0R4πr2GrM(r)ρ(r)dr,{displaystyle H_{mathrm {tot} }^{mathrm {grav} }=-int _{0}^{R}{frac {4pi r^{2}G}{r}}M(r),rho (r),dr,}
где M(r) — масса внутри радиуса r, ρ(r) — звёздная плотность на радиусе r, G — гравитационная постоянная, R — полный радиус звезды. Предполагая постоянную плотность звезды интегрирование по радиусу приводит к выражению
- Htotgrav=−3GM25R,{displaystyle H_{mathrm {tot} }^{mathrm {grav} }=-{frac {3GM^{2}}{5R}},}
где M — полная масса звезды. отсюда следует, что средняя потенциальная энергия одной частицы равна
- ⟨Hgrav⟩=HtotgravN=−3GM25RN,{displaystyle langle H^{mathrm {grav} }rangle ={frac {H_{mathrm {tot} }^{mathrm {grav} }}{N}}=-{frac {3GM^{2}}{5RN}},}
где N — число частиц в звезде. Большинство звёзд состоит главным образом из ионизированного водорода, тогда N равно приблизительно (M/mp), где mp — масса протона. Применение закона о равнораспределении даёт оценку температуры звезды
- ⟨r∂Hgrav∂r⟩=⟨−Hgrav⟩=kBT=3GM25RN.{displaystyle {Bigl langle }r{frac {partial H^{mathrm {grav} }}{partial r}}{Bigr rangle }=langle -H^{mathrm {grav} }rangle =k_{B}T={frac {3GM^{2}}{5RN}}.}
Если подставить в это выражение массу и радиус Солнца, то оценочная солнечная температура T составит 14 миллионов кельвинов, очень близко к температуре ядра Солнца (15 миллионов кельвинов). Правда здесь надо отметить, что Солнце по структуре гораздо сложнее, чем принято в этой упрощённой модели и её температура как и плотность изменяются сильно как функция радиуса, а такое хорошее согласие (≈7 % относительная ошибка) частично наше везение.[52]
Звездообразование |
Полученные выше формулы можно использовать для определения условий для звездообразования из гигантских молекулярных облаков.[53]
Местные колебания плотности в таких облаках могут привести к нестабильному состоянию, в котором облако сожмётся под собственной тяжестью. Такой коллапс происходит, когда теорема о равнораспределении или, эквивалентно, теорема о вириале больше не применимы, то есть, когда гравитационная потенциальная энергия в два раза превышает кинетическую энергию
- 3GM25R>3NkBT{displaystyle {frac {3GM^{2}}{5R}}>3Nk_{B}T}
Предполагая постоянную плотность ρ для облака формула
- M=43πR3ρ{displaystyle M={frac {4}{3}}pi R^{3}rho }
даёт оценку минимальной массы для зарождения звёзды , которая называется массой Джинса MJ
- MJ2=(5kBTGmp)3(34πρ){displaystyle M_{J}^{2}=left({frac {5k_{B}T}{Gm_{p}}}right)^{3}left({frac {3}{4pi rho }}right)}
Подставляя значения типичных масс в таких наблюдаемых облаках (T=150 К, ρ = 2⋅10−16 г/см³) даёт оценку минимальной массы равную 17 солнечным массам, которая согласуется с наблюдаемым звёздообразованием. Этот эффект известен как нестабильность Джинса. Он назван в честь британского физика Джеймса Джинса, который опубликовал описание этой нестабильности в 1902 году.[54]
Выводы |
Кинетическая энергия и распределение Максвелла—Больцмана |
Первоначальная формулировка теоремы о равнораспределении гласит, что в физической системе при термодинамическом равновесии каждая частица обладает одинаковой средней кинетической энергией, (3/2)kBT.[55] Это можно показать используя распределение Максвелла — Больцмана (см. выше рисунок распределения плотности вероятности скоростей молекул), которое является распределением вероятности
- f(v)=4π(m2πkBT)3/2v2exp(−mv22kBT){displaystyle f(v)=4pi left({frac {m}{2pi k_{B}T}}right)^{3/2}!!v^{2}exp {Bigl (}{frac {-mv^{2}}{2k_{B}T}}{Bigr )}}
для скорости частицы с массой m в системе, где скорость v — амплитуда vx2+vy2+vz2{displaystyle {sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}}

Распределение Максвелла — Больцмана применимо для системы состоящей из атомов и предполагает только что система частиц представляет собой канонический ансамбль, в частности, что кинетические энергии распределены в соответствии с множителем Больцмана при температуре T.[55] Средняя кинетическая энергия для частицы массы m задаётся интегральной формулой
- ⟨Hkin⟩=⟨12mv2⟩=∫0∞12mv2 f(v) dv=32kBT,{displaystyle langle H^{mathrm {kin} }rangle =langle {tfrac {1}{2}}mv^{2}rangle =int _{0}^{infty }{tfrac {1}{2}}mv^{2} f(v) dv={tfrac {3}{2}}k_{B}T,}
как и гласит теорема о равнораспределении. Тот же результат можно получить усредняя энергии частиц используя вероятность найти частицу в некотором энергетическом квантовом состоянии[44].
Квадратичные энергии и статистическая сумма |
Более обще, теорема о равнораспределении гласит, что любая степень свободы x, которая появляется в полной энергии H только как квадратичное слагаемое вида Ax², где A — постоянная, имеет среднюю энергию ½kBT в термодинамическом равновесии. В этом случае равнораспределение можно вывести из статистической суммы Z(β), где β=1/(kBT) — обычная обратная температура.[56] Интегрирование по переменной x даёт множитель
- Zx=∫−∞∞dx e−βAx2=πβA,{displaystyle Z_{x}=int _{-infty }^{infty }dx e^{-beta Ax^{2}}={sqrt {frac {pi }{beta A}}},}
в формуле для Z. Средняя энергия связанная с этим фактором дана выражением
- ⟨Hx⟩=−∂logZx∂β=12β=12kBT{displaystyle langle H_{x}rangle =-{frac {partial log Z_{x}}{partial beta }}={frac {1}{2beta }}={frac {1}{2}}k_{B}T}
как гласит теорема о равнораспределении.
Общие доказательства |
общие выводы теоремы о равнораспределении можно найти в многих учебниках по статистической механике как для микроканонического ансамбля[4][6] так и для канонического ансамбля[4][42]
Эти методы предполагают усреднение в фазовом пространстве системы, которое представляет собой симплектическое многообразие.
Для объяснения этих выводов нужно ввести следующие обозначения. Во первых, фазовое пространство описано в терминах обобщённых координат qj вместе с их сопряжёнными импульсами pj. Величины qj полностью описывают конфигурацию системы, в то же время величины (qj,pj) вместе полностью описывают её состояние.
Во вторых, вводят бесконечно малый объём
- dΓ=∏idqidpi{displaystyle dGamma =prod _{i}dq_{i}dp_{i}}
фазового пространства и используют его как объём Γ(E, ΔE) той части фазового пространства, где энергия системы H принимает значение в диапазоне энергий между E и E+ΔE:
- Γ(E,ΔE)=∫H∈[E,E+ΔE]dΓ.{displaystyle Gamma (E,Delta E)=int _{Hin left[E,E+Delta Eright]}dGamma .}
В этом выражении, ΔE очень мало, ΔE<<E. Аналогично, Σ(E) определён как полный объём фазового пространства, где энергия меньше чем E:
- Σ(E)=∫H<EdΓ.{displaystyle Sigma (E)=int _{H<E}dGamma .}
Из-за малости ΔE, следующее интегрирования эквивалентны
- ∫H∈[E,E+ΔE]…dΓ=ΔE∂∂E∫H<E…dΓ,{displaystyle int _{Hin left[E,E+Delta Eright]}ldots dGamma =Delta E{frac {partial }{partial E}}int _{H<E}ldots dGamma ,}
где точки представляют собой интегрируемое выражение. Из этого следует, что Γ пропорционален ΔE
- Γ=ΔE ∂Σ∂E=ΔE ρ(E),{displaystyle Gamma =Delta E {frac {partial Sigma }{partial E}}=Delta E rho (E),}
где ρ(E) — плотность состояний. По обычным определениям из статистической механики, энтропия S равна kB log Σ(E), и температура T определена как
- 1T=∂S∂E=kb∂logΣ∂E=kb1Σ∂Σ∂E.{displaystyle {frac {1}{T}}={frac {partial S}{partial E}}=k_{b}{frac {partial log Sigma }{partial E}}=k_{b}{frac {1}{Sigma }},{frac {partial Sigma }{partial E}}.}
Канонический ансамбль |
В каноническом ансамбле, система находится в тепловом равновесии с бесконечным тепловым резервуаром при температуре T (в кельвинах).[4][42] Вероятность каждого состояния в фазовом пространстве задаётся её множителем Больцмана умноженном на нормирующий множитель N{displaystyle {mathcal {N}}}
- N∫e−βH(p,q)dΓ=1,{displaystyle {mathcal {N}}int e^{-beta H(p,q)}dGamma =1,}
где β = 1/kBT. Интегрирование по частям для переменной в фазовом пространстве xk (которая может быть либо qk либо pk) между двумя пределами a и b приводит к уравнению
- N∫[e−βH(p,q)xk]xk=axk=bdΓk+N∫e−βH(p,q)xkβ∂H∂xkdΓ=1,{displaystyle {mathcal {N}}int left[e^{-beta H(p,q)}x_{k}right]_{x_{k}=a}^{x_{k}=b}dGamma _{k}+{mathcal {N}}int e^{-beta H(p,q)}x_{k}beta {frac {partial H}{partial x_{k}}}dGamma =1,}
где dΓk = dΓ/dxk, то есть, первое интегрирование не производится по xk. Первое слагаемое обычно равно нулю, потому, что xk равен нулю на пределах, или потому что энергия расходится на пределах. В этом случае теорема о равнорапределении немедленно следует из этого
- N∫e−βH(p,q)xk∂H∂xkdΓ=⟨xk∂H∂xk⟩=1β=kBT.{displaystyle {mathcal {N}}int e^{-beta H(p,q)}x_{k}{frac {partial H}{partial x_{k}}},dGamma ={Bigl langle }x_{k}{frac {partial H}{partial x_{k}}}{Bigr rangle }={frac {1}{beta }}=k_{B}T.}
Здесь, символ обозначающий усреднение ⟨…⟩{displaystyle langle ldots rangle }
Микроканонический ансамбль |
В микроканиническом ансамбле, система изолирована от остального мира, или по крайней мере слабо связана.[6] Отсюда следует, что её полная энергия постоянная величина. Пусть для определённости полная энергия H находиться между E и E+ΔE. Для данной энергии E и неопределённости ΔE, имеется область в фазовом пространстве Γ когда система имеет эту энергию, и вероятности каждого состояния в этой области фазового пространства равны, по определению микроканонического ансамбля. Из этих определений следует, что усреднение по переменным в фазовом пространстве xm (которые могут быть либо qk или pk) и xn задано в виде
- ⟨xm∂H∂xn⟩=1Γ∫H∈[E,E+ΔE]xm∂H∂xndΓ=ΔEΓ∂∂E∫H<Exm∂H∂xndΓ=1ρ∂∂E∫H<Exm∂(H−E)∂xndΓ,{displaystyle {begin{aligned}{Bigl langle }x_{m}{frac {partial H}{partial x_{n}}}{Bigr rangle }&={frac {1}{Gamma }},int _{Hin left[E,E+Delta Eright]}x_{m}{frac {partial H}{partial x_{n}}},dGamma \&={frac {Delta E}{Gamma }},{frac {partial }{partial E}}int _{H<E}x_{m}{frac {partial H}{partial x_{n}}},dGamma \&={frac {1}{rho }},{frac {partial }{partial E}}int _{H<E}x_{m}{frac {partial left(H-Eright)}{partial x_{n}}},dGamma ,end{aligned}}}
где последнее равенство следует из того, что E не зависит от xn. Интегрирование по частям приводит к соотношению
- ∫H<Exm∂(H−E)∂xndΓ=∫H<E∂∂xn(xm(H−E))dΓ−∫H<Eδmn(H−E)dΓ=δmn∫H<E(E−H)dΓ,{displaystyle {begin{aligned}int _{H<E}x_{m}{frac {partial (H-E)}{partial x_{n}}},dGamma &=int _{H<E}{frac {partial }{partial x_{n}}}{bigl (}x_{m}(H-E){bigr )},dGamma -int _{H<E}delta _{mn}(H-E)dGamma \&=delta _{mn}int _{H<E}(E-H),dGamma ,end{aligned}}}
поскольку первое слагаемое справа в первой строчке равно нулю (его можно записать как интеграл H — E по гиперпространству, где H = E).
Подставляя этот результат в предыдущее уравнение даёт
- ⟨xm∂H∂xn⟩=δmn1ρ∂∂E∫H<E(E−H)dΓ=δmn1ρ∫H<EdΓ=δmnΣρ.{displaystyle {Bigl langle }x_{m}{frac {partial H}{partial x_{n}}}{Bigr rangle }=delta _{mn}{frac {1}{rho }},{frac {partial }{partial E}}int _{H<E}left(E-Hright),dGamma =delta _{mn}{frac {1}{rho }},int _{H<E},dGamma =delta _{mn}{frac {Sigma }{rho }}.}
Поскольку ρ=∂Σ∂E{displaystyle rho ={frac {partial Sigma }{partial E}}}
- ⟨xm∂H∂xn⟩=δmn(1Σ∂Σ∂E)−1=δmn(∂logΣ∂E)−1=δmnkBT.{displaystyle {Bigl langle }x_{m}{frac {partial H}{partial x_{n}}}{Bigr rangle }=delta _{mn}{Bigl (}{frac {1}{Sigma }}{frac {partial Sigma }{partial E}}{Bigr )}^{-1}=delta _{mn}{Bigl (}{frac {partial log Sigma }{partial E}}{Bigr )}^{-1}=delta _{mn}k_{B}T.}
Таким образом мы получили общую формулировку теоремы о равнораспределении
- ⟨xm∂H∂xn⟩=δmnkBT,{displaystyle {Bigl langle }x_{m}{frac {partial H}{partial x_{n}}}{Bigr rangle }=delta _{mn}k_{B}T,}
которая была использована в применениях показанных выше.
Применимость |
Требование эргодичности |
Закон равнораспределения выполняется только для эргодичных систем находящихся в термодинамическом равновесии, что подразумевает, что все состояния с равной энергией должны быть заполнены с равной вероятностью.[6] Следовательно, должен быть возможен обмен энергией между различными её формами в пределах системы, или с внешним тепловым резервуаром в каноническом ансамбле. Число физических систем, для которых известно строгое доказательство эргодичности мало. Наиболее известный пример — система твёрдых шаров Якова Синая.[57] Изученные требования для изолированных систем с гарантированной эргодичностью и, таким образом, равнораспределение, обеспечили предпосылки для современной теории хаоса динамических систем. Хаотическая гамильтова система не обязательно должна быть эргодичной, хотя это обычно хорошее приближение.[58]
Система связанных гармонических осцилляторов — обычно цитируемый контрпример, поскольку энергия не делится между различными её формами и равнораспределение не выполняется в микроканоническом ансамбле.[58] Если система изолирована от остального мира, энергия в каждой нормальной моде постоянна и энергия не передаётся от одной моды к другой. Следовательно, закон равнораспределения не выполняется для такой системы, поскольку количество энергии в каждой нормальной моде определяется её начальным значением. Если присутствуют достаточно сильные нелинейные слагаемые в энергии, то она может перераспределяться между нормальными модами, приводя к тому что закон равнораспределения выполняется. Однако, теорема Колмогорова — Арнольда — Мозера утверждает, что если нелинейные возмущения должны быть достаточно сильны для перераспределения энергии; в противном случае, когда они малы, энергия останется сконцентрирована в, по крайней мере, некоторых из мод.
Ограничения, накладываемые квантовой механикой |
Закон равнораспределения нарушается, когда тепловая энергия kBT становится значительно меньше, чем расстояние между энергетическими уровнями. Равнораспределение не работает, потому что предположение о непрерывном спектре энергетических уровней, которое использовалось выше при выводе закона равнораспределения, больше не является хорошим приближением.[4][6] Исторически, невозможность объяснить с помощью классической теоремы о равнораспределении удельную теплоёмкость и излучение абсолютно чёрного тела послужила основной причиной осознания того факта, что необходима новые теории материи и излучения, а именно квантовая механика и квантовая теория поля.[8]
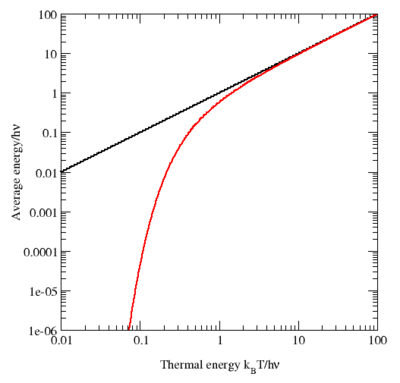
График средней энергии квантовомеханического осциллятора (красная кривая) в зависимости от температуры в логарифмическом масштабе. Для сравнения значение предсказанное теоремой о равнораспределении показаны чёрным. При высокой температуре две кривые имеют очень хорошее согласие, но при низких температурах, когда kBT << hν, квантовомеханическое значение уменьшается намного быстрее. Это приводит к решению проблемы ультрофиолетовой катастрофы: для данной температуры энергия высокочастотных мод (когда hν >> kBT) почти обращается в ноль
Для иллюстрации нарушения теоремы о равнораспределении, рассмотрим среднюю энергию одиночного (квантового) гармонического осциллятора, который обсуждался выше для классического случая. Его квантовые уровни заданы в виде En = nhν, где h — постоянная Планка, ν — фундаментальная частота осциллятора, и n — целое положительное число. Вероятность того, что заданный уровень энергии окажется заполнен в каноническом ансамбле задаётся его множителем Больцмана
- P(En)=e−nβhνZ,{displaystyle P(E_{n})={frac {e^{-nbeta hnu }}{Z}},}
где β = 1/kBT и знаменатель Z — статистическая сумма, здесь геометрический ряд
- Z=∑n=0∞e−nβhν=11−e−βhν.{displaystyle Z=sum _{n=0}^{infty }e^{-nbeta hnu }={frac {1}{1-e^{-beta hnu }}}.}
Его средняя энергия задаётся в виде
- ⟨H⟩=∑n=0∞EnP(En)=1Z∑n=0∞nhν e−nβhν=−1Z∂Z∂β=−∂logZ∂β.{displaystyle langle Hrangle =sum _{n=0}^{infty }E_{n}P(E_{n})={frac {1}{Z}}sum _{n=0}^{infty }nhnu e^{-nbeta hnu }=-{frac {1}{Z}}{frac {partial Z}{partial beta }}=-{frac {partial log Z}{partial beta }}.}
Подставляя формулу для Z приводит к искомому результату[6]
- ⟨H⟩=hνe−βhν1−e−βhν.{displaystyle langle Hrangle =hnu {frac {e^{-beta hnu }}{1-e^{-beta hnu }}}.}
При высоких температурах, когда тепловая энергия kBT много больше расстояния hν между энергетическими уровнями, экспоненциальный показатель βhν оказывается много меньше единицы и средняя энергия становится равной kBT, в соответствии с законом о равнораспределении (см. график). Однако, при низких температурах, когда hν >> kBT, средняя энергия стремится к нулю — высокочастотные уровни энергии «вымораживаются» (см. график). Другой пример, возбуждённые электронные состояния атома водорода не вносят вклада в удельную теплоёмкость газа при комнатной температуре, потому что тепловая энергия kBT (приблизительно 0.025 эВ) много меньше, чем расстояние между основным состоянием и первым возбуждённым уровнем (приблизительно 10 эВ).
Аналогичные рассмотрения применимы вне зависимости от того, больше ли расстояние между энергетическими уровнями, чем тепловая энергия. Например, эта посылка была использована Альбертом Эйнштейном, чтобы разрешить ультрафиолетовую катастрофу излучения абсолютно чёрного тема.[59] Парадокс возникает из-за того, что имеется бесконечное число независимых мод электромагнитного поля в замкнутом контейнере, каждая из которых трактуется как гармонический осциллятор. Если каждая электромагнитная мода обладает средней энергией kBT, тогда в контейнере будет содержатся бесконечная энергия.[59][60] Однако, по причине обсуждаемой выше, средняя энергия в высокочастотных модах стремится к нулю когда частота стремится к бесконечности; более того, планковский закон излучения абсолютно чёрного тела, который следует из экспериментально найденного распределения энергии по модам следует из этой же причины.[59]
Есть более тонкие квантовые эффекты, которые могут привести к коррекциям теоремы равнораспределения, такие как тождественность частиц и непрерывные симметрии. Эффекты неразличимости частиц могут доминировать при больших концентрациях и низких температурах. Например, валентные электроны в металле могут иметь среднюю кинетическую энергию несколько электронвольт, которая соответствует температуре в десятки тысяч градусов. В состоянии, в котором плотность достаточно высокая, что принцип запрета Паули делает неприменимым классический подход, называется вырожденный ферми-газ. Такие газы важны в структуре белых карликов и нейтронных звёзд. При низких температурах формируется фермионный аналог конденсата Бозе — Эйнштейна (в котором много тождественных частиц занимают основное энергетическое состояние); такие сверхтекучие электроны ответственны за сверхпроводимость.
См. также |
- Молекулярно-кинетическая теория
- Статистическая механика
- Квантовая статистика
Примечания |
↑ Здесь, как можно видеть, термин степень свободы используется в том "термодинамическом" смысле, который несколько отличается от обычного в физике, а именно (в варианте, приведенном в данной статье): отдельными степенями свободы рассматриваются координатные (ответственные за потенциальную энергию) и скоростные (ответственные за кинетическую), тогда как обычно координату и соответствующую ей скорость относят к одной и той же степени свободы. Легко видеть, что в данном контексте такое изменение смысла термина оправдано простотой формулировки теоремы. Заметим, что координаты, потенциальная энергия от которых не зависит (хотя бы в первом приближении) квадратично (а это координаты, соответствующие поступательному и вращательному движению молекулы), дают пренебрежимый вклад в потенциальную энергию, хотя обычный вклад ½kBT в кинетическую энергию. Выделенность колебательных степеней свободы, потенциальная энергия которых квадратична (хотя бы приближенно), состоит в том, что в колебательных системах, близких к гармоничности, потенциальная энергия равна кинетической при свободных колебаниях.
↑ 12 Kundt, A.; Warburg E. (1876). “Über die specifische Wärme des Quecksilbergases (On the specific heat of mercury gases)”. Annalen der Physik. 157: 353—369. Используется устаревший параметр|coauthors=(справка).mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em} (нем.)
↑ Fact Sheet on Uranium Enrichment U.S. Nuclear Regulatory Commission. Accessed 30th April 2007
↑ 123456789101112 Pathria, R. K. Statistical Mechanics. — Pergamon Press, 1972. — P. pp. 43–48, 73–74. — ISBN 0-08-016747-0.
↑ 123 Goldstein, H. Classical Mechanics. — 2nd. ed. — Addison-Wesley, 1980. — ISBN 0-201-02918-9.
↑ 123456789 Huang, K. Statistical Mechanics. — 2nd ed. — John Wiley and Sons, 1987. — P. pp. 136–138. — ISBN ISBN 0-471-81518-7.
↑ 12 Mandl, F. Statistical Physics. — John Wiley and Sons, 1971. — P. pp. 213–219. — ISBN ISBN 0-471-56658-6.
↑ 1234 Pais, A. Subtle is the Lord. — Oxford University Press, 1982. — ISBN 0-19-853907-X.
↑ 12 Tolman, R. C. (1918). “A General Theory of Energy Partition with Applications to Quantum Theory”. Physical Review. 11: 261—275.
↑ Miedl M, Garcia M, Bamforth C (2005). “Haze formation in model beer systems”. J. Agric. Food Chem. 53 (26): 10161—5. DOI:10.1021/jf0506941. PMID 16366710.
↑ Mason, M; Weaver W (1924). “The Settling of Small Particles in a Fluid”. Physical Review. 23: 412—426. DOI:10.1103/PhysRev.23.412. Используется устаревший параметр|coauthors=(справка)
↑ Brush, S. G. The Kind of Motion We Call Heat, Volume 1. — Amsterdam : North Holland, 1976. — P. 134–159. — ISBN 978-0444870094.
↑ Brush, S. G. The Kind of Motion We Call Heat, Volume 2. — Amsterdam : North Holland, 1976. — P. 336–339. — ISBN 978-0444870094.
↑ Waterston, JJ (1846/1893). “On the physics of media that are composed of free and elastic molecules in a state of motion”. Roy. Soc. Proc. 5: 604. Проверьте дату в|year=(справка на английском)(абстракт). Полностью не опубликован до Philos. Trans. R. Soc. London. A183: 1—79. 1893.|title=пусто или отсутствует (справка) Переиздан The collected scientific papers of John James Waterston / J. S. Haldane. — Edinburgh : Oliver & Boyd, 1928.
↑ Waterston, J. J. Thoughts on the Mental Functions. — 1843. (перепечатано в его Papers, 3, 167, 183.)
↑ Waterston, J. J. (1851). British Association Reports. 21: 6.|title=пусто или отсутствует (справка)
Основная статья Уотерстона была написана и подана в 1845 году в Королевское общество. После отказа напечатать работу общество также отказалось от возврата манускрипта и сохранило его среди других статей в архиве. Манускрипт был найден в 1891 году Лордом Рэлеем, который раскритиковал референта за то, что тот не распознал значительность работы Уотерстона. Уотерстону удалось опубликовать свои идеи в 1851 году, и поэтому он опередил Максвелла в изложении первой версии теоремы равнораспределения.
↑ Maxwell, J. C. Illustrations of the Dynamical Theory of Gases // The Scientific Papers of James Clerk Maxwell / W. D. Niven. — New York : Dover, 2003. — P. Vol.1, pp. 377–409. — ISBN 978-0486495606. Read by Prof. Maxwell at a Meeting of the British Association at Aberdeen on 21 September 1859.
↑ Boltzmann, L. (1871). “Einige allgemeine Sätze über Wärmegleichgewicht (Some general statements on thermal equilibrium)”. Wiener Berichte. 63: 679—711. (нем.) В этой предварительной работе Больцман показал, что средняя полная кинетическая энергия равна средней полной потенциальной энергии, когда на систему действуют внешние гармонические силы.
↑ Boltzmann, L. (1876). “Über die Natur der Gasmoleküle (On the nature of gas molecules)”. Wiener Berichte. 74: 553—560. (нем.)
↑ 12 McQuarrie, DA. Statistical Mechanics. — revised 2nd ed. — University Science Books, 2000. — P. pp. 91–128. — ISBN ISBN 978-1-891389-15-3.
↑ Petit, A. T.; Dulong P. L. (1819). “Recherches sur quelques points importants de la théorie de la chaleur (Studies on key points in the theory of heat)”. Annales de Chimie et de Physique. 10: 395—413. Используется устаревший параметр|coauthors=(справка) (фр.)
↑ Dewar, J. (1872). “The Specific Heat of Carbon at High Temperatures”. Philosophical Magazine. 44: 461.
↑ Weber, HF (1872). “Die specifische Wärme des Kohlenstoffs (The specific heat of carbon)”. Annalen der Physik. 147: 311—319. (нем.)
↑ Weber, H. F. (1875). “Die specifische Wärmen der Elemente Kohlenstoff, Bor und Silicium (The specific heats of elemental carbon, boron, and silicon)”. Annalen der Physik. 154: 367—423, 553—582. (недоступная ссылка) (нем.)
↑ de la Rive, A.; Marcet F. (1840). “Quelques recherches sur la chaleur spécifique (Some research on specific heat)”. Annales de Chimie et de Physique. 75: 113—144. Используется устаревший параметр|coauthors=(справка) (фр.)
↑ Regnault, H. V. (1841). “Recherches sur la chaleur spécifique des corps simples et des corps composés (deuxième Mémoire) (Studies of the specific heats of simple and composite bodies)”. Annales de Chimie et de Physique. 1 (3me Série): 129—207. (фр.) Read at l’Académie des Sciences on 11 January 1841.
↑ Wigand, A. (1907). “Über Temperaturabhängigkeit der spezifischen Wärme fester Elemente (On the temperature dependence of the specific heats of solids)”. Annalen der Physik. 22: 99—106. (нем.)
↑ 12 Wüller, A. Lehrbuch der Experimentalphysik (Textbook of Experimental Physics). — Leipzig : Teubner, 1896. — P. Vol. 2, 507ff. (нем.)
↑ 12 Eucken, A. (1912). “Die Molekularwärme des Wasserstoffs bei tiefen Temperaturen (The molecular specific heat of hydrogen at low temperatures)”. Sitzungsberichte der königlichen Preussischen Akademie der Wissenschaften. 1912: 141—151. (нем.)
↑ 12 Maxwell, J. C. On the Dynamical Evidence of the Molecular Constitution of Bodies // The Scientific Papers of James Clerk Maxwell / WD Niven. — Cambridge : At the University Press, 1890. — P. Vol.2, pp.418–438. Лекция прочитанная профессором Максвеллом Химическому обществу 18 февраля 1875 года.
↑ 12 Kittel, C. Introduction to Solid State Physics. — New York : John Wiley and Sons, 1996. — P. 151–156. — ISBN ISBN 978-0-471-11181-8.
↑ Boltzmann, L. (1895). “On certain Questions of the Theory of Gases”. Nature. 51: 413—415.
↑ Thomson, W. Baltimore Lectures. — Baltimore : Johns Hopkins University Press, 1904. — P. Sec. 27. Перепечатана в 1987 году издательством MIT Press под названием Kelvin’s Baltimore Lectures and Modern Theoretical Physics: Historical and Philosophical Perspectives (Robert Kargon and Peter Achinstein, editors). ISBN 978-0-262-11117-1
↑ Rayleigh, J. W. S. (1900). “The Law of Partition of Kinetic Energy”. Philosophical Magazine. 49: 98—118.
↑ Einstein, A. (1907). “Die Plancksche Theorie der Strahlung und die Theorie der spezifischen Wärme (The Planck theory of radiation and the theory of specific heat)”. Annalen der Physik. 22: 180—190. (нем.)
↑ Einstein, A. (1907). “Berichtigung zu meiner Arbeit: 'Die Plancksche Theorie der Strahlung und die Theorie der spezifischen Wärme' (Correction to previous article)”. Annalen der Physik. 22: 800. (нем.)
↑ Einstein, A. (1911). “Eine Beziehung zwischen dem elastischen Verhalten and der spezifischen Wärme bei festen Körpern mit einatomigem Molekül (A connection between the elastic behavior and the specific heat of solids with single-atom molecules)”. Annalen der Physik. 34: 170—174. (нем.)
↑ Einstein, A. (1911). “Bemerkung zu meiner Arbeit: 'Eine Beziehung zwischen dem elastischen Verhalten and der spezifischen Wärme bei festen Körpern mit einatomigem Molekül' (Comment on previous article)”. Annalen der Physik. 34: 590. (нем.)
↑ Einstein, A. (1911). “Elementare Betrachtungen über die thermische Molekularbewegung in festen Körpern (Elementary observations on the thermal movements of molecules in solids)”. Annalen der Physik. 35: 679—694. (нем.)
↑ Nernst, W. (1910). “Untersuchungen über die spezifische Wärme bei tiefen Temperaturen. II. (Investigations into the specific heat at low temperatures)”. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 1910: 262—282. (нем.)
↑ Hermann, Armin. The Genesis of Quantum Theory (1899–1913). — original title: Frühgeschichte der Quantentheorie (1899–1913), translated by Claude W. Nash. — Cambridge, MA : The MIT Press, 1971. — P. pp. 124—145. — ISBN 0-262-08047-8, .
↑ 123 Tolman, R. C. The Principles of Statistical Mechanics. — New York : Dover Publications, 1938. — P. pp. 93–98. — ISBN 0-486-63896-0.
↑ Clausius, R. (1870). “Ueber einen auf die Wärme anwendbaren mechanischen Satz”. Annalen der Physik. 141: 124—130. (нем.)
Clausius, R. J. E. (1870). “On a Mechanical Theorem Applicable to Heat”. Philosophical Magazine, Ser. 4. 40: 122—127.
↑ 12 L. Vu-Quoc, Configuration integral (statistical mechanics) Архивировано 11 октября 2008 года., 2008.
↑ McQuarrie, D. A. Statistical Mechanics. — revised 2nd ed. — University Science Books, 2000. — P. pp. 254–264. — ISBN 978-1891389153.
↑ 12 Tolman, R. C. Statistical Mechanics, with Applications to Physics and Chemistry. — Chemical Catalog Company, 1927. — P. pp. 76–77.
↑ Terletskii, Y. P. Statistical Physics. — translated: N. Fröman. — Amsterdam : North-Holland, 1971. — P. pp. 83-84. — ISBN 0-7204-0221-2, .
↑ Collins, G. W. The Virial Theorem in Stellar Astrophysics. — Pachart Press, 1978.
↑ Chandrasekhar, S. An Introduction to the Study of Stellar Structure. — Chicago : University of Chicago Press, 1939. — P. pp. 49–53.
↑ Kourganoff, V. Introduction to Advanced Astrophysics. — Dordrecht, Holland : D. Reidel, 1980. — P. pp. 59–60, 134–140, 181–184.
↑ Chiu, H.-Y. Stellar Physics, volume I. — Waltham, MA : Blaisdell Publishing, 1968. — ISBN .
↑ Noyes, R. W. The Sun, Our Star. — Cambridge, MA : Harvard University Press, 1982. — ISBN 0-674-85435-7.
↑ Ostlie, D. A. An Introduction to Modern Stellar Astrophysics. — Reading, MA : Addison-Wesley, 1996. — ISBN 0-201-59880-9.
↑ Jeans, J. H. (1902). “The Stability of a Spherical Nebula”. Phil. Trans. A. 199: 1—53. DOI:10.1098/rsta.1902.0012.
↑ 12 McQuarrie, D. A. Statistical Mechanics. — revised 2nd ed. — University Science Books, 2000. — P. pp. 121–128. — ISBN 978-1891389153.
↑ Callen, H. B. Thermodynamics and an Introduction to Thermostatistics. — New York : John Wiley and Sons, 1985. — P. pp. 375–377. — ISBN 0-471-86256-8.
↑ Arnold, V. I. Théorie ergodique des systèms dynamiques. — Gauthier-Villars, Paris. (фр.) (English edition: Benjamin-Cummings, Reading, Mass. 1968), 1967.
↑ 12 Reichl, L. E. A Modern Course in Statistical Physics. — 2nd ed. — Wiley Interscience, 1998. — P. 326–333. — ISBN 978-0471595205.
↑ 123 Einstein, A. (1905). “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (A Heuristic Model of the Creation and Transformation of Light)”. Annalen der Physik. 17: 132—148. DOI:10.1002/andp.19053220607. (недоступная ссылка) (нем.). An English translation is available from Wikisource.
↑ Rayleigh, J. W. S. (1900). “Remarks upon the Law of Complete Radiation”. Philosophical Magazine. 49: 539—540.
Литература |
- K. Huang. Statistical Mechanics. — 2nd ed. — John Wiley and Sons, 1987. — P. 136—138. — ISBN 0-471-81518-7.
- A. I. Khinchin. Mathematical Foundations of Statistical Mechanics / Пер. G. Gamow. — New York: Dover Publications, 1949. — P. 93—98. — ISBN 0-486-63896-0.
- L. D. Landau, E. M. Lifshitz. Statistical Physics, Part 1. — 3rd ed. — Pergamon Press, 1980. — P. 129—132. — ISBN 0-08-023039-3.
- F. Mandl. Statistical Physics. — John Wiley and Sons, 1971. — P. 213—219. — ISBN 0-471-56658-6.
- F. Mohling. Statistical Mechanics: Methods and Applications. — John Wiley and Sons, 1982. — P. 137—139, 270—273, 280, 285—292. — ISBN 0-470-27340-2.
- R. K. Pathria. Statistical Mechanics. — Pergamon Press, 1972. — P. 43—48, 73—74. — ISBN 0-08-016747-0.
- W. Pauli. Pauli Lectures on Physics: Volume 4. Statistical Mechanics. — MIT Press, 1973. — P. 27—40. — ISBN 0-262-16049-8.
- R. C. Tolman. Statistical Mechanics, with Applications to Physics and Chemistry. — Chemical Catalog Company, 1927. — P. 72—81.
- R. C. Tolman. The Principles of Statistical Mechanics. — New York: Dover Publications, 1938. — P. 93—98. — ISBN 0-486-63896-0.
Ссылки |
Апплет, демонстрирующий закон равнораспределения в реальном времени для смеси одноатомных и двухатомных газов
The equipartition theorem in stellar physics, written by Nir J. Shaviv, an associate professor at the Racah Institute of Physics in the Hebrew University of Jerusalem.






















































![{displaystyle Gamma (E,Delta E)=int _{Hin left[E,E+Delta Eright]}dGamma .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1d30011a6e9f81ffb1ec8d5f853eb11512962c8)

![{displaystyle int _{Hin left[E,E+Delta Eright]}ldots dGamma =Delta E{frac {partial }{partial E}}int _{H<E}ldots dGamma ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dacf6f8ccd4ccf04ffa00683a62e9327772e5f0f)



![{displaystyle {mathcal {N}}int left[e^{-beta H(p,q)}x_{k}right]_{x_{k}=a}^{x_{k}=b}dGamma _{k}+{mathcal {N}}int e^{-beta H(p,q)}x_{k}beta {frac {partial H}{partial x_{k}}}dGamma =1,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e941a978fe3d56ab99364c732bd077bb21eee1e)

![{displaystyle {begin{aligned}{Bigl langle }x_{m}{frac {partial H}{partial x_{n}}}{Bigr rangle }&={frac {1}{Gamma }},int _{Hin left[E,E+Delta Eright]}x_{m}{frac {partial H}{partial x_{n}}},dGamma \&={frac {Delta E}{Gamma }},{frac {partial }{partial E}}int _{H<E}x_{m}{frac {partial H}{partial x_{n}}},dGamma \&={frac {1}{rho }},{frac {partial }{partial E}}int _{H<E}x_{m}{frac {partial left(H-Eright)}{partial x_{n}}},dGamma ,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaed7c2b326b93b2548e32655ffc2945954a1b23)







