Шестиугольник




Шестиугольник — многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы.




Содержание






  • 1 Площадь шестиугольника без самопересечений


  • 2 Выпуклый шестиугольник


  • 3 Правильный шестиугольник


  • 4 Звездчатые шестиугольники


  • 5 См. также


  • 6 Примечания





Площадь шестиугольника без самопересечений |


Площадь шестиугольника без самопересечений, заданного координатами вершин, определяется по общей для многоугольников формуле.



Выпуклый шестиугольник |


Выпуклым шестиугольником называется шестиугольник, такой, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.


Сумма внутренних углов выпуклого шестиугольника равна 720°.


∑i=16αi=(6−2)⋅180∘=4⋅180∘=720∘{displaystyle sum _{i=1}^{6}alpha _{i}=(6-2)cdot 180^{circ }=4cdot 180^{circ }=720^{circ }}{displaystyle sum _{i=1}^{6}alpha _{i}=(6-2)cdot 180^{circ }=4cdot 180^{circ }=720^{circ }}

Доказано[1], что в любом достаточно большом множестве точек в общем положении содержится выпуклый пустой шестиугольник. Но существуют сколь угодно большие множества точек в общем положении, в которых нет выпуклого пустого семиугольника[2]. Вопрос о необходимом числе точек по сей день остаётся открытым. Известно, что требуется не менее 30 точек[3]. А если справедлива гипотеза Эрдёша-Секереша о многоугольниках, то не более 129[4].




Правильный шестиугольник



Правильный шестиугольник |


Основная статья: Правильный шестиугольник

Правильным называется шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.




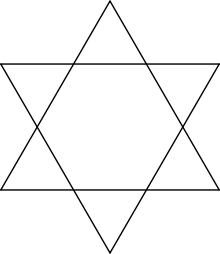
Гексаграмма



Звездчатые шестиугольники |


Основная статья: Гексаграмма (символ)

Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника, называется звёздчатым. Помимо правильного существует ещё один звёздчатый шестиугольник, состоящий из двух правильных треугольников — гексаграмма или звезда Давида.



См. также |



  • Пчелиные соты


  • Теорема Паскаля и теорема Брианшона

  • Неравенство Птолемея

  • Гексагональные шахматы

  • Гигантский гексагон

  • Задача со счастливым концом



Примечания |





  1. ↑ Nicolás, Carlos M. (2007), "The empty hexagon theorem", Discrete and Computational Geometry Т. 38 (2): 389–397, DOI 10.1007/s00454-007-1343-6 


  2. ↑ Horton, J. D. (1983), "Sets with no empty convex 7-gons", Canadian Mathematical Bulletin Т. 26 (4): 482–484, DOI 10.4153/CMB-1983-077-8 


  3. ↑ Overmars, M. (2003), "Finding sets of points without empty convex 6-gons", Discrete and Computational Geometry Т. 29 (1): 153–158, DOI 10.1007/s00454-002-2829-x 


  4. ↑ Gerken, Tobias (2008), "Empty convex hexagons in planar point sets", Discrete and Computational Geometry Т. 39 (1–3): 239–272, DOI 10.1007/s00454-007-9018-x 









Формула
Это заготовка статьи по математике. Вы можете помочь проекту, дополнив её.








-

Popular posts from this blog

Михайлов, Христо

Image
В Википедии есть статьи о других людях с фамилиями Михайлов и Попов. Христо Михайлов Попов болг. Христо Михайлов Попов Памятник в Монтане Дата рождения 18 апреля 1893 ( 1893-04-18 ) Место рождения Видин, Княжество Болгария Дата смерти 8 февраля 1944 ( 1944-02-08 ) (50 лет) Место смерти София, Третье Болгарское царство Принадлежность Болгария   Болгария Род войск сухопутные войска Годы службы 1912—1944 Звание генерал-полковник Командовал Народно-освободительная повстанческая армия Болгарии Сражения/войны Первая Балканская война Вторая Балканская война Первая мировая война Сентябрьское восстание Вторая мировая война Связи Иван Попов (брат) Дом-музей Христо Попова Христо Михайлов Попов , в Болгарии известный как Христо Михайлов , (болг. Христо Михайлов Попов ; 18 апреля 1893, Видин — 8 февраля 1944, София) — болгарский военный и государственный деятель, участник и руководитель Движения Сопротивления в Болгарии...
Read more

Центральная группа войск

Image
Центральная группа войск (ЦГВ) Эмблема ВС Годы существования 1945—1955 1968—1991 Страна СССР Подчинение МО СССР Входит в РККА (СА), Вооружённых Сил СССР. Численность превышала 300 000 человек Дислокация Австрия и Венгрия (1945—1955), Чехословакия (1968—1991) Командиры Известные командиры Командующие войсками , См. список. 9 мая в штаб-квартире ЦГВ , 1984 год. Парк в ЦГВ , 1985 год. Магазин «Детский мир» в Миловице, ЦГВ , 1985 год. Центральная группа войск (ЦГВ)  — оперативно-стратегическое объединение (группа войск) Советских ВС, дважды существовавшее в период после окончания Великой Отечественной войны: в 1945—1955 годах дислоцировалась на территории Австрии и Венгрии; в период с 24 октября 1968 по 21 июня 1991 дислоцировалась в Чехословакии. Содержание 1 Центральная группа войск (1-го формирования) 1.1 Командующие (ЦГВ 1-го формирования): 2 Центральная группа войск (2-го формирования) 3 ...
Read more

Троллейбус

Image
Троллейбус Привод Электрический двигатель Период с 1882 года Область применения общественный транспорт, городской или междугородный Инфраструктура автомобильная дорога, контактная сеть Содержание 1 Этимология 2 История 3 Инфраструктура и организация движения 3.1 Дорожная сеть 3.2 Электропитание 3.3 Контактная сеть 3.4 Остановки 3.5 Троллейбусные предприятия 3.6 Разворотные пункты 3.7 График и расписания 3.8 Скорость движения 3.9 Способы оплаты проезда 4 Подвижной состав 5 Устройство троллейбуса 5.1 Шасси и компоновка 5.1.1 Кузов 5.1.2 Салон 5.1.3 Номерной знак и маршрутоуказатели 5.2 Ходовая часть и трансмиссия 5.3 Электрооборудование 5.3.1 Тяговый электродвигатель 5.3.2 Система управления двигателем 5.3.3 Системы автономного хода 5.3.4 Вспомогательная электроаппаратура 5.3.5 Электробезопасность 5.4 Токоприёмники 5.5 Тормозная система ...
Read more