Теория струн

Multi tool use
Тео́рия струн — направление теоретической физики, изучающее динамику взаимодействия не точечных частиц[1], а одномерных протяжённых объектов, так называемых квантовых струн[2]. Теория струн сочетает в себе идеи квантовой механики и теории относительности, поэтому на её основе, возможно, будет построена будущая теория квантовой гравитации[3][4].

Взаимодействие в микромире: диаграмма Фейнмана в стандартной модели и её аналог в теории струн
Теория струн основана на гипотезе[5] о том, что все элементарные частицы и их фундаментальные взаимодействия возникают в результате колебаний и взаимодействий ультрамикроскопических квантовых струн на масштабах порядка планковской длины 10−35 м[2]. Данный подход, с одной стороны, позволяет избежать таких трудностей квантовой теории поля, как перенормировка[6], а с другой стороны, приводит к более глубокому взгляду на структуру материи и пространства-времени[6].
Квантовая теория струн возникла в начале 1970-х годов в результате осмысления формул Габриэле Венециано[7], связанных со струнными моделями строения адронов. Середина 1980-х и середина 1990-х ознаменовались бурным развитием теории струн, ожидалось, что в ближайшее время на основе теории струн будет сформулирована так называемая «единая теория», или «теория всего»[4], поискам которой Эйнштейн безуспешно посвятил десятилетия[8].
Но, несмотря на математическую строгость и целостность теории, пока не найдены варианты экспериментального подтверждения теории струн[2]. Возникшая для описания адронной физики, но не вполне подошедшая для этого, теория оказалась в своего рода экспериментальном вакууме описания всех взаимодействий.
Одна из основных проблем при попытке описать процедуру редукции струнных теорий из размерности 26 или 10[9] в низкоэнергетическую физику размерности 4 заключается в большом количестве вариантов компактификаций дополнительных измерений на многообразия Калаби — Яу и на орбифолды, которые, вероятно, являются частными предельными случаями пространств Калаби — Яу[10]. Большое число возможных решений с конца 1970-х и начала 1980-х годов создало проблему, известную под названием «проблема ландшафта»[11], в связи с чем некоторые учёные сомневаются, заслуживает ли теория струн статуса научной[12].
Несмотря на эти трудности, разработка теории струн стимулировала развитие математических формализмов, в основном — алгебраической и дифференциальной геометрии, топологии, а также позволила глубже понять структуру предшествующих ей теорий квантовой гравитации[2]. Развитие теории струн продолжается, и есть надежда[2], что недостающие элементы струнных теорий и соответствующие феномены будут найдены в ближайшем будущем, в том числе в результате экспериментов на Большом адронном коллайдере[13].
Содержание
1 Основные положения
2 История
2.1 Струны в адронной физике
2.2 Бозонная теория струн
2.3 Суперструнные революции
3 Основные свойства
3.1 Классификация струнных теорий
3.2 Дуальности
3.2.1 Т-дуальность
3.2.2 S-дуальность
3.2.3 U-дуальность
3.3 Дополнительные измерения
3.3.1 Компактификация
3.3.2 Локализация
4 Проблемы
4.1 Возможность критического эксперимента
4.2 Фальсифицируемость и проблема ландшафта
4.3 Вычислительные проблемы
4.4 Проблема масштаба «зернистости» пространства
5 Текущие исследования
5.1 Изучение свойств чёрных дыр
5.2 Струнная космология
5.3 Косвенные предсказания
6 См. также
7 Примечания
8 Литература
8.1 Научно-популярная
8.2 Монографии, научные статьи и учебники
8.3 Критика теории струн
9 Ссылки
Основные положения |
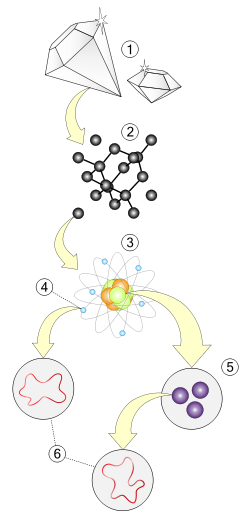
Уровни строения мира:
1. Макроскопический уровень — вещество
2. Молекулярный уровень
3. Атомный уровень — протоны, нейтроны и электроны
4. Субатомный уровень — электрон
5. Субатомный уровень — кварки
6. Струнный уровень
Если бы существовал явный механизм экстраполяции струн в низкоэнергетическую физику, то теория струн представила бы нам все фундаментальные частицы и их взаимодействия в виде ограничений на спектры возбуждений нелокальных одномерных объектов. Характерные размеры компактифицированных струн чрезвычайно малы, порядка 10−33 см (порядка планковской длины)[14], поэтому они недоступны наблюдению в эксперименте[2]. Аналогично колебаниям струн музыкальных инструментов спектральные составляющие струн возможны только для определённых частот (квантовых амплитуд). Чем больше частота, тем больше энергия, накопленная в таком колебании[15], и, в соответствии с формулой E=mc², тем больше масса частицы, в роли которой проявляет себя колеблющаяся струна в наблюдаемом мире. Параметром, аналогичным частоте для осциллятора, для струны является квадрат массы[16].
Непротиворечивые и самосогласованные квантовые теории струн возможны лишь в пространствах высшей размерности (больше четырёх, учитывая размерность, связанную со временем). В связи с этим в струнной физике открыт вопрос о размерности пространства-времени[17]. То, что в макроскопическом (непосредственно наблюдаемом) мире дополнительные пространственные измерения не наблюдаются, объясняется в струнных теориях одним из двух возможных механизмов: компактификация этих измерений — скручивание до размеров порядка планковской длины, или локализация всех частиц многомерной вселенной (мультивселенной) на четырёхмерном мировом листе, который и являет собой наблюдаемую часть мультивселенной. Предполагается, что высшие размерности могут проявляться во взаимодействиях элементарных частиц при высоких энергиях, однако до сих пор экспериментальные указания на такие проявления отсутствуют.
При построении теории струн различают подход первичного и вторичного квантования. Последний оперирует понятием струнного поля − функционала на пространстве петель, подобно квантовой теории поля. В формализме первичного квантования математическими методами описывается движение пробной струны во внешних струнных полях, при этом не исключается взаимодействие между струнами, в том числе распад и объединение струн. Подход первичного квантования связывает теорию струн с обычной теорией поля на мировой поверхности[4].
Наиболее реалистичные теории струн в качестве обязательного элемента включают суперсимметрию, поэтому такие теории называются суперструнными[18]. Набор частиц и взаимодействий между ними, наблюдающийся при относительно низких энергиях, практически воспроизводит структуру стандартной модели в физике элементарных частиц, причём многие свойства стандартной модели получают изящное объяснение в рамках суперструнных теорий. Тем не менее до сих пор нет принципов, с помощью которых можно было бы объяснить те или иные ограничения струнных теорий, чтобы получить некое подобие стандартной модели[19].
В середине 1980-х годов Майкл Грин и Джон Шварц пришли к выводу, что суперсимметрия, являющаяся центральным звеном теории струн, может быть включена в неё не одним, а двумя способами: первый — это суперсимметрия мировой поверхности струны[4], второй — пространственно-временная суперсимметрия[20]. В своей основе данные способы введения суперсимметрии связывают методы конформной теории поля со стандартными методами квантовой теории поля[21][22]. Технические особенности реализации данных способов введения суперсимметрии обусловили возникновение пяти различных теорий суперструн — типа I, типов IIA и IIB, и двух гетеротических струнных теорий[23]. Возникший в результате этого всплеск интереса к теории струн был назван «первой суперструнной революцией». Все эти модели формулируются в 10-мерном пространстве-времени, однако различаются струнными спектрами и калибровочными группами симметрии. Заложенная в 1970-х и развитая в 1980-х годах конструкция 11-мерной супергравитации[24], а также необычные топологические двойственности фазовых переменных в теории струн в середине 1990-х привели ко «второй суперструнной революции». Выяснилось, что все эти теории, на самом деле, тесно связаны друг с другом благодаря определённым дуальностям[25]. Было высказано предположение, что все пять теорий являются различными предельными случаями единой фундаментальной теории, получившей название М-теории. В настоящее время ведутся поиски адекватного математического языка для формулировки этой теории[19].
История |
Струны в адронной физике |

Леонард Сасскинд
Струны как фундаментальные объекты были первоначально введены в физику элементарных частиц для объяснения особенностей строения адронов, в частности пионов.
В 1960-х годах была обнаружена зависимость между спином адрона и его массой (график Чу — Фраучи)[26][27]. Это наблюдение привело к созданию теории Редже, в которой разные адроны рассматривались не как элементарные частицы, а как различные проявления единого протяжённого объекта — реджеона. В последующие годы усилиями Габриэле Венециано, Йоитиро Намбу, Холгера Бех Нильсена и Леонарда Сасскинда была выведена формула для рассеяния реджеонов и была дана струнная интерпретация протекающих при этом явлений.
В 1968 году Габриэле Венециано и Махико Судзуки при попытке анализа процесса столкновений пи-мезонов (пионов) обнаружили, что амплитуда парного рассеивания высокоэнергетических пионов весьма точно описывается одной из бета-функций, введённых Леонардом Эйлером в 1730 году. Позже было установлено, что амплитуда парного пионного рассеивания может быть разложена в бесконечный ряд, начало которого совпадает с формулой Венециано — Судзуки[28].
В 1970 году Йоитиро Намбу, Тэцуо Гото, Холгер Бех Нильсен и Леонард Сасскинд выдвинули идею, что взаимодействие между сталкивающимися пионами возникает вследствие того, что эти пионы соединяет «бесконечно тонкая колеблющаяся нить». Полагая, что эта «нить» подчиняется законам квантовой механики, они вывели формулу, совпадающую с формулой Венециано — Судзуки. Таким образом, появились модели, в которых элементарные частицы представляются в виде одномерных струн, которые вибрируют на определённых нотах (частотах)[28].
С наступлением эры квантовой хромодинамики научное сообщество утратило интерес к теории струн в адронной физике вплоть до 1980-х годов[2].
Бозонная теория струн |
К 1974 году стало ясно, что струнные теории, основанные на формулах Венециано, реализуются в размерности пространства большей, чем 4: модель Венециано и модель Шапиро — Вирасоро (S-V) в размерности 26, а модель Рамо́на — Невьё — Шварца (R-N-S) в 10, и все они предсказывают тахионы[29]. Скорость тахионов превышает скорость света в вакууме, а потому их существование противоречит принципу причинности, который, в свою очередь нарушается в микромире. Таким образом, не имеется никаких убедительных (в первую очередь, экспериментальных) доказательств существования тахиона, равно как и логически неуязвимых опровержений[30]. На данный момент считается более предпочтительным не использовать идею тахионов при построении физических теорий. Решение проблемы тахионов основано на работах по пространственно-временной глобальной (не зависящей от координат) суперсимметрии Весса и Зумино (1974 год)[31]. В 1977 году Глиоцци, Шерк и Олив (GSO проекция) ввели в модель R-N-S специальную проекцию для струнных переменных, которая позволила устранить тахион и по существу давала суперсимметричную струну[32]. В 1981 году Грину и Шварцу удалось описать GSO проекцию в терминах D-мерной суперсимметрии и чуть позже ввести принцип устранения аномалий в теориях струн[33].
В 1974 году Джон Шварц и Жоэль Шерк, а также независимо от них Тамиаки Ёнэя, изучая свойства некоторых струнных вибраций, обнаружили, что они в точности соответствуют свойствам гипотетической частицы − кванта гравитационного поля, которая называется гравитон[34]. Шварц и Шерк утверждали, что теория струн первоначально потерпела неудачу потому, что физики недооценили её масштаб[19]. На основе данной модели была создана теория бозонных струн[4], которая по-прежнему остаётся первым вариантом теории струн, который преподают студентам[35]. Эта теория формулируется в терминах действия Полякова, с помощью которого можно предсказывать движение струны в пространстве и времени. Процедура квантования действия Полякова приводит к тому, что струна может вибрировать различными способами и каждый способ её вибрации генерирует отдельную элементарную частицу. Масса частицы и характеристики её взаимодействия определяются способом вибрации струны, или своеобразной «нотой», которая извлекается из струны. Получающаяся таким образом гамма называется спектром масс теории струн.
Первоначальные модели включали как открытые струны, то есть нити, имеющие два свободных конца, так и замкнутые, то есть петли. Эти два типа струн ведут себя по-разному и генерируют два различных спектра. Не все современные теории струн используют оба типа, некоторые обходятся только замкнутыми струнами.
Теория бозонных струн не лишена проблем. Прежде всего, теория обладает фундаментальной нестабильностью, которая предполагает распад самого пространства-времени. Кроме того, как следует из её названия, спектр частиц ограничивается только бозонами. Несмотря на то, что бозоны представляют собой важный ингредиент мироздания, Вселенная состоит не только из них. Также она предсказывает несуществующую частицу с отрицательным квадратом массы — тахион[16]. Исследования того, каким образом можно включить в спектр теории струн фермионы, привело к понятию суперсимметрии — теории взаимосвязи бозонов и фермионов, которая теперь имеет самостоятельное значение. Теории, включающие в себя фермионные вибрации струн, называются суперструнными теориями[36].
Суперструнные революции |

Эдвард Виттен, один из лидеров исследований М-теории
В 1984—1986 гг. физики поняли, что теория струн могла бы описать все элементарные частицы и взаимодействия между ними, и сотни учёных начали работу над теорией струн как наиболее перспективной идеей объединения физических теорий.
Первой суперструнной революцией стало открытие в 1984 году Майклом Грином и Джоном Шварцем явления сокращения аномалий в теории струн типа I. Механизм этого сокращения носит название механизма Грина — Шварца. Другие значительные открытия, например, открытие гетеротической струны, были сделаны в 1985 г.[19]

Хуан Малдасена в Гарварде
В середине 1990-х Эдвард Виттен, Джозеф Полчински и другие физики обнаружили веские доказательства того, что различные суперструнные теории представляют собой различные предельные случаи не разработанной пока 11-мерной М-теории. Это открытие ознаменовало собой вторую суперструнную революцию.
Последние исследования теории струн (точнее, М-теории) затрагивают D-браны, многомерные объекты, существование которых вытекает из включения в теорию открытых струн[19].
В 1997 году Хуан Малдасена обнаружил взаимосвязь между теорией струн и калибровочной теорией, которая называется N=4 суперсимметричная теория Янга — Миллса[4]. Эта взаимосвязь, которая называется AdS/CFT-соответствием (сокращение терминов anti de Sitter space — «пространство анти-де-Ситтера», и conformal field theory — «конформная теория поля»), привлекла большой интерес струнного сообщества и сейчас активно изучается[37]. Данное «AdS/CFT-соответствие» является конкретной реализацией голографического принципа, который имеет далеко идущие следствия в отношении чёрных дыр, локальности и информации в физике, а также природы гравитационного взаимодействия.
В 2003 году разработка ландшафта теории струн, означающего существование в теории струн экспоненциально большого числа неэквивалентных ложных вакуумов[38][39][40], дало начало дискуссии о том, что в итоге может предсказать теория струн и каким образом может измениться струнная космология (подробнее см. ниже).
Основные свойства |
Среди многих свойств теории струн особенно важны три нижеследующих:
Гравитация и квантовая механика являются неотъемлемыми принципами устройства Вселенной, и поэтому любой проект единой теории обязан включать и то, и другое. В теории струн это реализуется.- Исследования на протяжении XX века показали, что существуют и другие ключевые концепции, — многие из которых были проверены экспериментально, — являющиеся центральными для нашего понимания Вселенной. В их числе — спин, существование поколений частиц материи и частиц-переносчиков взаимодействия, калибровочная симметрия, принцип эквивалентности, нарушение симметрии[41] и суперсимметрия. Всё это естественным образом вытекает из теории струн.
- В отличие от более общепринятых теорий, таких, как стандартная модель с её 19 свободными параметрами, которые могут подгоняться для обеспечения согласия с экспериментом, в теории струн свободных параметров нет[2][19].
Классификация струнных теорий |
| Тип |
Число измерений пространства-времени |
Характеристика |
|---|---|---|
| Бозонная |
26 |
Описывает только бозоны, нет фермионов; струны как открытые, так и замкнутые; основной недостаток: частица с мнимой массой, движущаяся со скоростью, большей скорости света, — тахион |
| I |
10 |
Включает суперсимметрию; струны как открытые, так и замкнутые; отсутствует тахион; групповая симметрия — SO(32) |
| IIA |
10 |
Включает суперсимметрию; струны только замкнутые; отсутствует тахион; безмассовые фермионы нехиральны |
| IIB |
10 |
Включает суперсимметрию; струны только замкнутые; отсутствует тахион; безмассовые фермионы хиральны |
| HO |
10 |
Включает суперсимметрию; струны только замкнутые; отсутствует тахион; теория гетеротическая: струны, колеблющиеся по часовой стрелке, отличаются от струн, колеблющихся против; групповая симметрия — SO(32) |
| HE |
10 |
Включает суперсимметрию; струны только замкнутые; отсутствует тахион; теория гетеротическая: струны, колеблющиеся по часовой стрелке, отличаются от струн, колеблющихся против; групповая симметрия — E8×E8 |
Несмотря на то, что понимание деталей суперструнных теорий требует серьёзной математической подготовки, некоторые качественные свойства квантовых струн можно понять на интуитивном уровне. Так, квантовые струны, как и обычные струны, обладают упругостью, которая считается фундаментальным параметром теории. Упругость квантовой струны тесно связана с её размером. Рассмотрим замкнутую струну, к которой не приложены никакие силы. Упругость струны будет стремиться стянуть её в более мелкую петлю вплоть до размера точки. Однако это нарушило бы один из фундаментальных принципов квантовой механики — принцип неопределённости Гейзенберга. Характерный размер струнной петли получится в результате балансирования между силой упругости, сокращающей струну, и эффектом неопределённости, растягивающим струну.
Благодаря протяжённости струны решается проблема ультрафиолетовых расходимостей в квантовой теории поля, и, следовательно, вся процедура регуляризации и перенормировки перестаёт быть математическим трюком и обретает физический смысл. Действительно, в квантовой теории поля бесконечные значения амплитуд взаимодействия возникают в результате того, что две частицы могут сколь угодно близко подойти друг к другу. В теории струн это уже невозможно: слишком близко расположенные струны сливаются в струну[6].
Дуальности |
В середине 1980-х было установлено, что суперсимметрия, являющаяся центральным звеном теории струн[42], может быть включена в неё не одним, а пятью различными способами, что приводит к пяти различным теориям: типа I, типов IIA и IIB, и две гетеротические струнные теории. Можно предположить, что только одна из них могла претендовать на роль «теории всего», причём та, которая при низких энергиях и компактифицированных шести дополнительных измерениях согласовывалась бы с реальными наблюдениями. Оставались открытыми вопросы о том, какая именно теория более адекватна и что делать с остальными четырьмя теориями[19]С. 126.
В ходе второй суперструнной революции было показано, что такое представление неверно: все пять суперструнных теорий тесно связаны друг с другом, являясь различными предельными случаями единой 11-мерной фундаментальной теории (М-теория)[19][43].
Все пять суперструнных теорий связаны друг с другом преобразованиями, называемыми дуальностями[44]. Если две теории связаны между собой преобразованием дуальности (дуальным преобразованием), это означает, что каждое явление и качество из одной теории в каком-нибудь предельном случае имеет свой аналог в другой теории, а также имеется некий своеобразный «словарь» перевода из одной теории в другую[45].
То есть дуальности связывают и величины, которые считались различными или даже взаимоисключающими. Большие и малые масштабы, сильные и слабые константы связи — эти величины всегда считались совершенно чёткими пределами поведения физических систем как в классической теории поля, так и в квантовой. Струны, тем не менее, могут устранять различия между большим и малым, сильным и слабым.
Т-дуальность |
Т-дуальность связана с симметрией в теории струн, применимой к струнным теориям типа IIA и IIB и двум гетеротическим струнным теориям. Преобразования Т-дуальности действуют в пространствах, в которых по крайней мере одна область имеет топологию окружности. При таком преобразовании радиус R этой области меняется на 1/R, и «намотанные»[46] состояния струн меняются на высокоимпульсные струнные состояния в дуальной теории. Таким образом, меняя импульсные моды и винтовые моды струны, можно переключаться между крупным и мелким масштабом[47].
Другими словами связь теории типа IIA с теорией типа IIB означает, что их можно компактифицировать на окружность, а затем, поменяв винтовые и импульсные моды, а значит, и масштабы, можно увидеть, что теории поменялись местами. То же самое верно и для двух гетеротических теорий[48].
S-дуальность |
S-дуальность (сильно-слабая дуальность) − эквивалентность двух квантовых теорий поля, теории струн и M-теории. Преобразование S-дуальности заменяет физические состояния и вакуум с константой связи[49]g одной теории на физические состояния и вакуум с константой связи 1 / g другой, дуальной первой теории. Благодаря этому оказывается возможным использовать теорию возмущений, которая справедлива для теорий с константой связи g много меньшей 1, по отношению к дуальным теориям с константой связи g много большей 1[48]. Суперструнные теории связаны S-дуальностью следующим образом: суперструнная теория типа I S-дуальна гетеротической SO(32) теории, а теория типа IIB S-дуальна самой себе.
U-дуальность |
Существует также симметрия, связывающая преобразования S-дуальности и T-дуальности. Она называется U-дуальностью и наиболее часто встречается в контексте так называемых U-дуальных групп симметрии в М-теории, определённых на конкретных топологических пространствах. U-дуальность представляет собой объединение в этих пространствах S-дуальности и T-дуальности, которые, как можно показать на D-бране, не коммутируют друг с другом[50].
Дополнительные измерения |
Интригующим предсказанием теории струн является многомерность Вселенной. Ни теория Максвелла, ни теории Эйнштейна не дают такого предсказания, поскольку предполагают число измерений заданным (в теории относительности их четыре). Первым, кто добавил пятое измерение к эйнштейновским четырём, оказался немецкий математик Теодор Калуца (1919 год)[51]. Обоснование ненаблюдаемости пятого измерения (его компактности) было предложено шведским физиком Оскаром Клейном в 1926 году[52].
Требование согласованности теории струн с релятивистской инвариантностью (лоренц-инвариантностью) налагает жёсткие требования на размерность пространства-времени, в котором она формулируется. Теория бозонных струн может быть построена только в 26-мерном пространстве-времени, а суперструнные теории — в 10-мерном[17].
Поскольку мы, согласно специальной теории относительности, существуем в четырёхмерном пространстве-времени[53][54], необходимо объяснить, почему остальные дополнительные измерения оказываются ненаблюдаемыми. В распоряжении теории струн имеется два таких механизма.
Компактификация |

Проекция 6-мерного пространства Калаби — Яу, полученная с помощью Mathematica
Первый из них заключается в компактификации дополнительных 6 или 7 измерений, то есть замыкание их на себя на таких малых расстояниях, что они не могут быть обнаружены в экспериментах. Шестимерное разложение моделей достигается с помощью пространств Калаби — Яу.
Классическая аналогия, используемая при рассмотрении многомерного пространства, — садовый шланг[55]. Если наблюдать шланг с достаточно далёкого расстояния, будет казаться, что он имеет только одно измерение — длину. Но если приблизиться к нему, обнаруживается его второе измерение — окружность. Истинное движение муравья, ползающего по поверхности шланга, двумерно, однако издалека оно нам будет казаться одномерным. Дополнительное измерение доступно наблюдению только с относительно близкого расстояния, поэтому и дополнительные измерения пространства Калаби — Яу доступны наблюдению только с чрезвычайно близкого расстояния, то есть практически не обнаруживаемы.
Локализация |
Другой вариант — локализация — состоит в том, что дополнительные измерения не столь малы, однако в силу ряда причин все частицы нашего мира локализованы на четырёхмерном листе в многомерной вселенной (мультивселенной) и не могут его покинуть. Этот четырёхмерный лист (брана) и есть наблюдаемая часть мультивселенной. Поскольку мы, как и вся наша техника, состоим из обычных частиц, то мы в принципе неспособны взглянуть вовне.
Единственная возможность обнаружить присутствие дополнительных измерений — гравитация. Гравитация, будучи результатом искривления пространства-времени, не локализована на бране, и потому гравитоны и микроскопические чёрные дыры могут выходить вовне. В наблюдаемом мире такой процесс будет выглядеть как внезапное исчезновение энергии и импульса, уносимых этими объектами.
Проблемы |
Возможность критического эксперимента |
Теория струн нуждается в экспериментальной проверке, однако ни один из вариантов теории не даёт однозначных предсказаний, которые можно было бы проверить в критическом эксперименте. Таким образом, теория струн находится пока в «зачаточной стадии»: она обладает множеством привлекательных математических особенностей и может стать чрезвычайно важной в понимании устройства Вселенной, но требуется дальнейшая разработка для того, чтобы принять её или отвергнуть. Поскольку теорию струн, скорее всего, нельзя будет проверить в обозримом будущем в силу технологических ограничений, некоторые учёные сомневаются, заслуживает ли данная теория статуса научной, поскольку, по их мнению, она не является фальсифицируемой в попперовском смысле[12][56][57].
Разумеется, это само по себе не является основанием считать теорию струн неверной. Часто новые теоретические конструкции проходят стадию неопределённости, прежде чем, на основании сопоставления с результатами экспериментов, признаются или отвергаются (см., например, уравнения Максвелла[58]). Поэтому и в случае теории струн требуется либо развитие самой теории, то есть методов расчёта и получения выводов, либо развитие экспериментальной науки для исследования ранее недоступных величин.
Фальсифицируемость и проблема ландшафта |
В 2003 году выяснилось[59], что существует множество способов свести 10-мерные суперструнные теории к 4-мерной эффективной теории поля. Сама теория струн не давала критерия, с помощью которого можно было бы определить, какой из возможных путей редукции предпочтителен. Каждый из вариантов редукции 10-мерной теории порождает свой 4-мерный мир, который может напоминать, а может и отличаться от наблюдаемого мира. Всю совокупность возможных реализаций низкоэнергетического мира из исходной суперструнной теории называют ландшафтом теории.
Оказывается, количество таких вариантов поистине огромно. Считается, что их число составляет как минимум 10100, вероятнее — около 10500; не исключено, что их вообще бесконечное число[60].
В течение 2005 года неоднократно высказывались предположения[61], что прогресс в этом направлении может быть связан с включением в эту картину антропного принципа[62]: человек существует именно в такой Вселенной, в которой его существование возможно.
Вычислительные проблемы |
С математической точки зрения ещё одна проблема состоит в том, что, как и квантовая теория поля, большая часть теории струн всё ещё формулируется пертурбативно (в терминах теории возмущений)[63]. Несмотря на то, что непертурбативные методы достигли за последнее время значительного прогресса, полной непертурбативной формулировки теории до сих пор нет.
Проблема масштаба «зернистости» пространства |
В результате экспериментов по обнаружению «зернистости» (степени квантования) пространства, которые состояли в измерении степени поляризации гамма-излучения, приходящего от далёких мощных источников, выяснилось, что в излучении гамма-всплеска GRB041219A, источник которого находится на расстоянии 300 млн световых лет, зернистость пространства не проявляется вплоть до размеров 10−48 м, что в 1014 раз меньше планковской длины[64]. Данный результат, по всей видимости, заставит пересмотреть внешние параметры струнных теорий[65][66][67].
Текущие исследования |
Изучение свойств чёрных дыр |
В 1996 г. струнные теоретики Эндрю Строминджер и Кумрун Вафа, опираясь на более ранние результаты Сасскинда и Сена, опубликовали работу «Микроскопическая природа энтропии Бекенштейна и Хокинга». В этой работе Строминджеру и Вафе удалось использовать теорию струн для нахождения микроскопических компонентов определённого класса чёрных дыр[68], а также для точного вычисления вкладов этих компонентов в энтропию. Работа была основана на применении нового метода, частично выходящего за рамки теории возмущений, которую использовали в 1980-х и в начале 1990-х гг. Результат работы в точности совпадал с предсказаниями Бекенштейна и Хокинга, сделанными более чем за двадцать лет до этого.
Реальным процессам образования чёрных дыр Строминджер и Вафа противопоставили конструктивный подход[2]. Суть в том, что они изменили точку зрения на образование чёрных дыр, показав, что их можно конструировать путём кропотливой сборки в один механизм точного набора бран, открытых во время второй суперструнной революции.
Строминджер и Вафа смогли вычислить число перестановок микроскопических компонентов чёрной дыры, при которых общие наблюдаемые характеристики, например масса и заряд, остаются неизменными. Тогда энтропия этого состояния по определению равна логарифму полученного числа — числа возможных микросостояний термодинамической системы. Затем они сравнили результат с площадью горизонта событий чёрной дыры — эта площадь пропорциональна энтропии чёрной дыры, как предсказано Бекенштейном и Хокингом на основе классического понимания[2], — и получили идеальное согласие[69]. По крайней мере, для класса экстремальных чёрных дыр Строминджеру и Вафе удалось найти приложение теории струн для анализа микроскопических компонентов и точного вычисления соответствующей энтропии.
Это открытие оказалось важным и убедительным аргументом в поддержку теории струн. Разработка теории струн до сих пор остаётся слишком грубой для прямого и точного сравнения с экспериментальными результатами, например, с результатами измерений масс кварков или электрона. Теория струн, тем не менее, даёт первое фундаментальное обоснование давно открытого свойства чёрных дыр, невозможность объяснения которого многие годы тормозила исследования физиков, работавших с традиционными теориями. Даже Шелдон Глэшоу, Нобелевский лауреат по физике и убеждённый противник теории струн в 1980-е гг., признался в интервью в 1997 г., что «когда струнные теоретики говорят о чёрных дырах, речь идёт едва ли не о наблюдаемых явлениях, и это впечатляет»[19].
Струнная космология |
Струнная космология — относительно новая и интенсивно развивающаяся область теоретической физики, в рамках которой осуществляются попытки использования уравнений теории струн для решения некоторых проблем, возникших в ранней космологической теории. Данный подход впервые использован в работах Габриэле Венециано[70], который показал, каким образом инфляционная модель Вселенной может быть получена из теории суперструн. Инфляционная космология предполагает существование некоторого скалярного поля, индуцирующего инфляционное расширение. В струнной космологии вместо этого вводится так называемое дилатонное поле[71][72], кванты которого, в отличие, например, от электромагнитного поля, не являются безмассовыми, поэтому влияние данного поля существенно лишь на расстояниях порядка размера элементарных частиц или на ранней стадии развития Вселенной[73].
Существует три основных пункта, в которых теория струн модифицирует стандартную космологическую модель. Во-первых, в духе современных исследований, всё более проясняющих ситуацию, из теории струн следует, что Вселенная должна иметь минимально допустимый размер. Этот вывод меняет представление о структуре Вселенной непосредственно в момент Большого взрыва, для которого в стандартной модели получается нулевой размер Вселенной. Во-вторых, понятие T-дуальности, то есть дуальности малых и больших радиусов (в его тесной связи с существованием минимального размера) в теории струн, имеет значение и в космологии[74]. В-третьих, число пространственно-временных измерений в теории струн больше четырёх, поэтому космология должна описывать эволюцию всех этих измерений. Вообще, особенность теории струн состоит в том, что в ней, по-видимому, геометрия пространства-времени не фундаментальна, а появляется в теории на больших масштабах или при слабой связи[75].
Косвенные предсказания |
Несмотря на то, что арена основных действий в теории струн недоступна прямому экспериментальному изучению[76][77], ряд косвенных предсказаний теории струн всё же можно проверить в эксперименте[78][79][80][81].
Во-первых, обязательным является наличие суперсимметрии. Ожидается, что запущенный 10 сентября 2008 года, но полноценно[82] вступивший в строй в 2010 году Большой адронный коллайдер сможет открыть некоторые суперсимметричные частицы.[13] Это будет серьёзной поддержкой теории струн[19].
Во-вторых, в моделях с локализацией наблюдаемой вселенной в мультивселенной изменяется закон гравитации тел на малых расстояниях. В настоящее время проводится ряд экспериментов, проверяющих с высокой точностью закон всемирного тяготения на расстояниях в сотые доли миллиметра[83]. Обнаружение отклонения от этого закона было бы ключевым аргументом в пользу суперсимметричных теорий.
В-третьих, в тех же самых моделях гравитация может становиться очень сильной уже на энергетических масштабах порядка нескольких ТэВ, что делает возможной её проверку на Большом адронном коллайдере. В настоящее время идёт активное исследование процессов рождения гравитонов и микроскопических чёрных дыр в таких вариантах теории.
Наконец, некоторые варианты теории струн приводят также и к наблюдательным астрофизическим предсказаниям. Суперструны (космические струны), D-струны или другие струнные объекты, растянутые до межгалактических размеров, обладают сильным гравитационным полем и могут выступать в роли гравитационных линз.
Кроме того, движущиеся струны должны создавать гравитационные волны, которые, в принципе, могут быть[84] обнаружены в экспериментах типа LIGO и VIRGO.
Они также могут создавать небольшие нерегулярности в реликтовом излучении, которые могут быть обнаружены в будущих экспериментах[19].
Этот раздел не завершён. |
См. также |
.mw-parser-output .ts-Родственные_проекты{background:#f8f9fa;border:1px solid #a2a9b1;clear:right;float:right;font-size:90%;margin:0 0 1em 1em;padding:.5em .75em}.mw-parser-output .ts-Родственные_проекты th,.mw-parser-output .ts-Родственные_проекты td{padding:.25em 0;vertical-align:middle}.mw-parser-output .ts-Родственные_проекты td{padding-left:.5em}
Теория струн на Викискладе |
- Квантовая гравитация
- Квантовая струна
- Космическая струна
М-теория (теория бран)- Суперсимметрия
- Теория бозонных струн
- Теория суперструн
- Нерешённые проблемы современной физики
Примечания |
↑ А. А. Комар. «Размер» элементарной частицы // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 3.
↑ 12345678910 Гросс, Дэвид. Грядущие революции в фундаментальной физике. Проект «Элементы», вторые публичные лекции по физике (25.04.2006).
↑ Sunil Mukhi (1999) «The Theory of Strings: A Detailed Introduction» (англ.).
↑ 123456 А. Ю. Морозов. Струн теория // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 5.
↑ Scherk J., Schwarz J.H. Dual models for non-hadrons (англ.) // Nucl.Phys. — 1974. — Vol. 81, iss. 1. — P. 118−144. — ISSN 0550-3213.
↑ 123 Морозов А. Ю.. Теория струн — что это такое? // УФН. — 1992. — Т. 162, № 8. — С. 83—175.
↑ Veneziano G., Nuovo Cim., 1968, 57A, 190 (также неопубликованная работа Suzuki M., 1968) (англ.).
↑ Б. Паркер. Мечта Эйнштейна. В поисках единой теории строения Вселенной. — М.: Амфора, 2000. — 333 с. — ISBN 5-8301-0198-Х.
↑ Polchinski, Joseph (1998). String Theory, Cambridge University Press (англ.).
↑ Каку, Мичио. Введение в теорию суперструн / пер. с англ. Г.Э. Арутюнова, А.Д. Попова, С.В. Чудова; под ред. И. Я. Арефьевой. — М.: Мир, 1999. — 624 с. — ISBN 5-03-002518-9..
↑ Yau S., Witten E. Simposium on Anomalies, Geometry and Topology, 1985, WS, Singhapur, Witten E.and others Nukl.Phys., 1985, B261, 678; 1986, B274, 286 (англ.).
↑ 12 Peter Woit. Теория струн: оценка (неизв.) (недоступная ссылка — история) (16 февраля 2001). Проверено 31 октября 2009. Архивировано 14 ноября 2004 года. arXiv:physics/0102051 (англ.).
↑ 12
Lisa Randall (2002). “Extra Dimensions and Warped Geometries” (PDF). Science. 296 (5572): 1422—1427. DOI:10.1126/science.1072567. PMID 12029124..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
↑ Для сравнения: струн по диаметру атома нужно примерно столько же, сколько атомов выстроить от Земли до Проксимы Центавра (ближайшая к Земле звезда, после Солнца. Альтернативный пример: клеточная ДНК находится в пространстве порядка 1 мкм³. Она, к сожалению, недоступна наблюдению, но если ДНК из хромосом одного ядра клетки человека вытянуть, то её длина составит около 20 м.
↑ С. В. Егерев. Струна // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: "Советская энциклопедия", 1988. — Т. 5.
↑ 12 Бухбиндер И. Л. Теория струн и объединение фундаментальных взаимодействий. // Соросовский образовательный журнал — 2001, № 7. — С. 99.
↑ 12 Барбашов, Б. М., Нестеренко, В. В. Суперструны — новый подход к единой теории фундаментальных взаимодействий // Успехи физических наук. Том 150, № 4. — М.: 1986, с. 489—524.
↑ Новая картина струнной теории (неизв.). Перевод "Официального Сайта Теории Суперструн". Проверено 1 октября 2009. Архивировано 22 августа 2011 года.
↑ 1234567891011 Грин Б. Элегантная Вселенная. Суперструны, скрытые размерности и поиски окончательной теории: Пер. с англ. / Под ред. В. О. Малышенко. — Изд. 3-е. — М.: Едиториал УРСС, 2007. — 288 с. — ISBN 5-484-00784-4.
↑ Green M.& Schwarz J. Phys. Lett. 1984, 149B, 117 (англ.).
↑ Polyakov A.M. Phys. Lett. 1981, 103B, 207, 211 (англ.).
↑ Belavin A.A., Polyakov A.M., Zamolodchikov A.B. Nucl. Phys. 1984, B241, 333 (англ.).
↑ S. James Gates, Jr., Ph.D., Superstring Theory: The DNA of Reality Архивная копия от 26 сентября 2007 на Wayback Machine «Lecture 23 — Can I Have that Extra Dimension in the Window?», 0:04:54, 0:21:00 (англ.).
↑ M. J. Duff, James T. Liu and R. Minasian Eleven Dimensional Origin of String/String Duality: A One Loop Test Center for Theoretical Physics, Department of Physics, Texas A&M University (англ.).
↑ Новая картина струнной теории (неизв.). Перевод "Официального Сайта Теории Суперструн". Проверено 1 октября 2009. Архивировано 22 августа 2011 года.
↑ Иванов, Игорь. Дифракция в физике элементарных частиц: рассказ первый Архивировано 25 января 2013 года.. Дневник в рамках проекта «Элементы», 15.09.2006.
↑ G. F. Chew and S. C. Frautschi, Phys. Rev. Letters, 8, 41 (1962); S. C. Frautschi, «Regge Poles and S-Matrix Theory», (W. A. Benjamin, New York, 1968) (англ.).
↑ 12 Левин, А. Струнный концерт для Вселенной // Популярная механика, март 2006.
↑ Shapiro J. Phys. Rev., 1971, 33В, 361. Virasoro M. Phys. Rev., 1969, 177, 2309. Ramond P. Phys. Rev., 1971, D3, 2415. Neveu A.& Schwarz J. Nucl. Phys., 1971, B31, 86.Lovelace C. Phys. Rev., 1974, 34B, 500 (англ.).
↑ Ю. П. Рыбаков. Тахион // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: "Советская энциклопедия", 1988. — Т. 5.
↑ Wess J., Zumino B. Nucl.Phys. 1974, B70, 39 (англ.).
↑ Gliozzi F., Sherk J., Ollive D. Nucl.Phys. 1977, B122, 253 (англ.).
↑ Green M.& Schwarz J. Nucl.Phys. 1981, B81, 253, Green M.& Schwarz J. Phys. Lett. 1984, 149B, 117 (англ.).
↑ В. И. Огиевецкий. Гравитон // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: "Советская энциклопедия", 1988. — Т. 1.
↑ Франке В.А. Учебный план физического факультета СПбГУ (неизв.). Санкт-Петербургский государственный университет. Проверено 6 января 2010. Архивировано 22 августа 2011 года.
↑ Vladimir G. Ivancevic, Tijana T. Ivancevic. Applied Differential Geometry: A Modern Introduction. — Sydney: World Scientific Publishing Company, 2007. — С. 41. — 1348 с. — ISBN 978-981-270-614-0. (англ.)
↑ Статистика опубликованных по тематике статей по годам: AdS/CFT correspondence on arxiv.org (англ.)
↑ S. Kachru, R. Kallosh, A. Linde and S. P. Trivedi, «de Sitter Vacua in String Theory», Phys.Rev. D68:046005, 2003, arXiv:hep-th/0301240 (англ.).
↑ M. Douglas, «The statistics of string / M theory vacua», JHEP 0305, 46 (2003). arXiv:hep-th/0303194 (англ.).
↑ S. Ashok and M. Douglas, «Counting flux vacua», JHEP 0401, 060 (2004) (англ.).
↑ Понижение симметрии, присущей системе, обычно связываемое с фазовым переходом.
↑ Ю. А. Гольфанд. Суперсимметрия // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: "Советская энциклопедия", 1988. — Т. 5.
↑ Эту ситуацию хорошо иллюстрирует притча о слоне.
↑ Aharony, O.; S.S. Gubser, J. Maldacena, H. Ooguri, Y. Oz (2000). “Large N Field Theories, String Theory and Gravity” (subscription required). Phys. Rept. 323: 183—386. DOI:10.1016/S0370-1573(99)00083-6. Используется устаревший параметр|coauthors=(справка) For other examples see: arXiv:hep-th/9802042 (англ.).
↑ В. А. Кудрявцев. Дуальность // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: "Советская энциклопедия", 1988. — Т. 2.
↑ Winding number может также переводиться как «число кручения», «число намоток», «винтовое число».
↑ Becker, K., Becker, M., and Schwarz, J. H. (2007). «String Theory and M-Theory: A Modern Introduction». Cambridge, UK: Cambridge University Press. (англ.).
↑ 12 Как между собой соотносятся различные теории струн? (неизв.). Перевод "Официального Сайта Теории Суперструн". Проверено 1 октября 2009. Архивировано 22 августа 2011 года.
↑ Константы связи (неизв.). Ядерная физика в Интернете (15 мая 2009). Проверено 1 октября 2009. Архивировано 22 августа 2011 года.
↑ Гуков, С. Г. Введение в струнные дуальности // Успехи физических наук. — М., 1998. — Т. 168, № 7. — С. 705—717.
↑ Wesson, Paul S. «Five-Dimensional Physics: Classical and Quantum Consequences of Kaluza-Klein Cosmology». — Singapore : World Scientific, 2006. — ISBN 9812566619. (англ.).
↑ Wesson, Paul S. «Space-Time-Matter, Modern Kaluza-Klein Theory». — Singapore : World Scientific, 1999. — ISBN 9810235887. (англ.).
↑ Naber, Gregory L. «The Geometry of Minkowski Spacetime». — New York : Springer-Verlag, 1992. — ISBN 0387978488. (англ.).
↑ Schutz, J., «Independent Axioms for Minkowski Spacetime», 1997. (англ.).
↑ Пол Девис. Суперсила. — М.: Мир, 1989, глава 10 («А не живём ли мы в одиннадцатимерном пространстве?»), параграф «Теория Калуцы-Клейна».
↑ Popper, Karl, «The Logic of Scientific Discovery», Basic Books, New York, NY, 1959. (англ.)
↑ Вячеслав Недогонов Вселенная — это воздушный шарик с ручкой // Новая газета. — 2017. — № 114. — 13.10.2017 — С. 18 — 19
↑ Электромагнитное излучение (неизв.). Krugosvet.ru. Проверено 2 октября 2009. Архивировано 22 августа 2011 года.
↑ См. в оригинале статью пионера теории струн Леонарда Сасскинда.
↑ M. Douglas, «The statistics of string / M theory vacua», JHEP 0305, 46 (2003). arXiv:hep-th/0303194; S. Ashok and M. Douglas, «Counting flux vacua», JHEP 0401, 060 (2004) (англ.).
↑ См. статью «Теория суперструн: в поисках выхода из кризиса».
↑ L. Susskind, «The anthropic landscape of string theory», arXiv:hep-th/0302219. (англ.).
↑ Д. В. Ширков. Квантовая теория поля // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: "Советская энциклопедия", 1988. — Т. 2.
↑ Согласно большинству теорий квантовой гравитации размер элементарного «зерна» должен соответствовать планковской длине.
↑ Попов Леонид. Самое точное измерение не выявило зернистости пространства (неизв.). Мембрана (04.07.2011). Проверено 5 июля 2011. Архивировано 22 августа 2011 года.
↑ Integral challenges physics beyond Einstein (англ.). ЕКА (30.06.2011). Проверено 7 июля 2011. Архивировано 22 августа 2011 года.
↑ P. Laurent, D. Gotz, P. Binetruy, S. Covino, A. Fernandez-Soto. Constraints on Lorentz Invariance Violation using INTEGRAL/IBIS observations of GRB041219A (англ.). arXiv.org (06.06.2011). Проверено 7 июля 2011.
↑ R. Dijkgraaf, E. Verlinde, H. Verlinde (1997) «5D Black Holes and Matrix Strings» (англ.).
↑ Черные дыры. Ответ из теории струн (неизв.). Перевод "Официального Сайта Теории Суперструн". Проверено 18 октября 2009. Архивировано 22 августа 2011 года.
↑ Veneziano, Gabriele The Myth of the Beginning of Time (неизв.) (May 2004). Архивировано 22 августа 2011 года. (англ.).
↑ H. Lu, Z. Huang, W. Fang and K. Zhang, «Dark Energy and Dilaton Cosmology». arXiv:hep-th/0409309 (англ.).
↑ F. Alvarenge, A. Batista and J. Fabris, «Does Quantum Cosmology Predict a Constant Dilatonic Field». arXiv:gr-qc/0404034 (англ.).
↑ Дилатонное поле (неизв.) (недоступная ссылка — история). Учебный центр «Архимед». Проверено 31 октября 2009.
↑ Космология. При чем же тут теория струн? (неизв.). Перевод "Официального Сайта Теории Суперструн". Проверено 1 октября 2009. Архивировано 22 августа 2011 года.
↑ Пространство, время и теория струн (неизв.). Перевод "Официального Сайта Теории Суперструн". Проверено 18 октября 2009. Архивировано 22 августа 2011 года.
↑ P. Woit (Columbia University) «String theory: An Evaluation», February 2001, arXiv:physics/0102051 (англ.).
↑ P. Woit, «Is String Theory Testable?» INFN Rome, March 2007 (англ.).
↑ H. Nastase, «The RHIC fireball as a dual black hole», BROWN-HET-1439, arXiv:hep-th/0501068, January 2005 (англ.).
↑ H. Nastase, «More on the RHIC fireball and dual black holes», BROWN-HET-1466, arXiv:hep-th/0603176, March 2006 (англ.).
↑ H. Liu, K. Rajagopal, U. A. Wiedemann, «An AdS/CFT Calculation of Screening in a Hot Wind», MIT-CTP-3757, arXiv:hep-ph/0607062 July 2006 (англ.).
↑ H. Liu, K. Rajagopal, U. A. Wiedemann, «Calculating the Jet Quenching Parameter from AdS/CFT», Phys.Rev.Lett.97:182301,2006 arXiv:hep-ph/0605178 (англ.).
↑ Правда, в половину максимальной мощности.
↑ Игорь Иванов. Проверка закона всемирного тяготения на субмиллиметровых расстояниях (неизв.). Scientific.ru (17 февраля 2001). Проверено 1 октября 2009. Архивировано 22 августа 2011 года.
↑ Денис Борн. Проект LIGO – поиск гравитационных волн (неизв.). 3dnews.ru (27 августа 2009). Проверено 16 октября 2009.
Литература |
Научно-популярная |
- На русском
Вайнберг С. Мечты об окончательной теории: физика в поисках самых фундаментальных законов природы: Пер. с англ = Steven Weinberg. Dreams of a Final Theory: The Search for the Fundamental Laws of Nature (1993). — М.: Едиториал УРСС / URSS, 2004. — 256 с. — ISBN 5-354-00526-4.. Теории струн посвящена 9-я глава «Контуры окончательной теории».- Грин Б. Элегантная Вселенная. Суперструны, скрытые размерности и поиски окончательной теории: Пер. с англ = Brian Greene. The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory (1999) / Под ред. В. О. Малышенко. — М.: Либроком, 2011. — 288 с. — ISBN 978-5-453-00011-1, 978-5-397-01575-2.
- Грин Б. Ткань космоса: Пространство, время и текстура реальности. Пер. с англ = Brian Greene. The Fabric of the Cosmos. Space, Time, and the Texture of Reality (2005) / Под ред. В. Малышенко, А. Панова ; перевод Б. Ишханова. — М.: Либроком, 2011. — 608 с. — ISBN 978-5-397-01966-8.
- Грин Б. Скрытая реальность: Параллельные миры и глубинные законы Космоса = The Hidden Reality: Parallel Universes and the Deep Laws of the Cosmos (2011). — М.: Едиториал УРСС / URSS, 2012. — ISBN 978-5-397-03333-6.
- Каку М. Параллельные миры. Об устройстве мироздания, высших измерениях и будущем Космоса: Пер. с англ = Michio Kaku. Parallel Worlds: A Journey Through Creation, Higher Dimensions and the Future of the Cosmos (2005). — М.: София, 2008. — 414 с. — ISBN 978-5-91250-520-1.
- Рэндалл Л. Закрученные пассажи: Проникая в тайны скрытых размерностей пространства = Randall, Lisa. (2005). Warped Passages. Unraveling the Mysteries of the Universe's Hidden Dimensions. / Волобуев И.П., Малышенко В.О. (под ред.). — М.: Едиториал УРСС / URSS, 2011. — 400 с. — ISBN 978-5-397-01371-0.
Сасскинд Л. Битва при черной дыре: Мое сражение со Стивеном Хокингом за мир, безопасный для квантовой механики = Susskind, Leonard. (2008). The Black Hole War. My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics. / перевод А. Сергеева. — СПб.: Питер, 2013. — 448 с. — 3500 экз. — ISBN 978-5-459-01837-0.. Теории струн посвящены главы с 18-й и далее.
Хокинг С. Краткая история времени: от Большого взрыва до чёрных дыр / Пер. с англ. Н. Смородинской. — СПб.: Амфора, 2004. — 268 с. — ISBN 5-94278-564-3.. Теории струн посвящена 10-я глава «Объединение физики».- Яу Ш., Надис С. Теория струн и скрытые измерения Вселенной: Пер. с англ = The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions (2010). — СПб.: Питер, 2012. — 400 с. — 3000 экз. — ISBN 978-5-459-00938-5, 978-0-465-02023-2.
- Кобзарев И. Ю., Манин Ю. И. Элементарные частицы. Диалоги физика и математика. — М.: Фазис, 1997. — С. 184—198. — 208 с. — ISBN 5-7036-0028-6.
- На английском
- Zimmerman Jones, Andrew; Robbins, Daniel. String Theory For Dummies. — Wiley Publishing, 2009. — 384 p. — ISBN 978-0470467244.
Монографии, научные статьи и учебники |
- На русском
- Барбашов Б. М., Нестеренко В. В.. Суперструны — новый подход к единой теории фундаментальных взаимодействий // УФН. — 1986. — Т. 150, № 4. — С. 489—524.
Инстантоны, струны и конформная теория поля / Сборник статей под ред. А. А. Белавина. — М.: Физматлит, 2002. — 448 с. — ISBN 5-9221-0303-2. (Проверено 27 апреля 2011) — Сборник состоит из 24 статей, посвящённых вопросам современной квантовой теории поля (конформная симметрия критических явлений, факторизованное рассеяние в двумерных теориях, инстантоны и монополи в калибровочных теориях, взаимодействие релятивистских струн) и её математическому анализу (алгебраическая топология, теория представлений бесконечномерных алгебр Ли, теория квантовых групп и др.). Статьи были ранее опубликованы в отечественных и зарубежных периодических изданиях в период 1970—1990 гг.
Бринк Л., Энно М. Принципы теории суперструн. — Новокузнецк: ИО НФМИ, 2000. — ISBN 5-8032-3337-4. — Изложение характеризуется достаточной степенью подробности, необходимой для изучения предмета читателями, не обладающими предварительными сведениями в этой области, но знакомыми с современной квантовой теорией поля, включая суперсимметрию.
Бухбиндер И. Л. Теория струн и объединение фундаментальных взаимодействий // Соросовский Образовательный Журнал. — 2001. — № 7. — С. 95—101. (Проверено 27 апреля 2011)
Горский А. С.. Калибровочные теории как теории струн: первые результаты // УФН. — 2005. — Т. 175, № 11. — С. 1145—1162. (Проверено 27 апреля 2011) — Рассматривается дуальность между калибровочными теориями и теорией струн в искривлённом пространстве. В качестве основного примера обсуждается дуальность между неабелевой конформной калибровочной теорией с N = 4 суперсимметрией и теорией замкнутой суперструны, распространяющейся в метрике AdS5 x S5. Показано, что дуальность в приближении супергравитации для струны позволяет вычислить различные характеристики калибровочной теории в режиме сильной связи.
Грин М., Шварц Дж., Виттен Э. Теория суперструн. — М.: Мир, 1990. — Т. 1, 2. — ISBN 5-03-001566-3. — Сборник научных статей лидеров теории струн периода первой суперструнной революции (1984—1986).
Грин М.. Теории суперструн в реальном мире = Superstring Theories in the Real World // New Scientist. 29 August 1985. P. 35. // УФН / Пер. с англ. А. А. Цейтлина.. — 1986. — Т. 150, № 4. — С. 577—579. (Проверено 27 апреля 2011) — краткий обзор начальной истории и состояния теории струн по итогам первой суперструнной революции от одного из отцов этой революции — Майкла Грина.
Гуков С. Г. Введение в струнные дуальности // УФН. — 1998. — Т. 168, № 7. — С. 705—717. (Проверено 27 апреля 2011) — даётся краткий обзор последних достижений в теории суперструн. Показано, как изучение струнных компактификаций, солитонов и D-бран приводит к понятиям S-, T- и U-дуальностей, которые связывают теории струн, до сих пор считавшиеся различными. Несмотря на то, что многие результаты всё ещё не имеют полного доказательства, понимание дуальностей, обсуждаемых в данном обзоре, помогает глубже понять многочисленные явления не только в теории струн, но и в геометрии, и в супергравитации.
До Тьен Ф. Некоторые методологические вопросы современной физики высоких энергий // Философские проблемы физики элементарных частиц (тридцать лет спустя). — М., 1994. — С. 199—215. (Проверено 27 апреля 2011)
Дубровский В. Н. Новая концепция пространства-времени на планковских расстояниях // Философские проблемы физики элементарных частиц (тридцать лет спустя). — М., 1994. — С. 73—86. (Проверено 27 апреля 2011)
Зарембо К. Л., Макеенко Ю. М.. Введение в матричные модели супеpструн // УФН. — 1998. — Т. 168, № 1. — С. 3—27. (Проверено 27 апреля 2011) — представлено введение в матричные модели суперструн и M-теории. Рассматривается матричная теория Бэнкса, Фишлера, Шенкера и Сасскинда, которая имеет вид суперсимметричной матричной квантовой механики. Обсуждаются две суперсимметричные матричные модели, являющиеся непертурбативной формулировкой суперструн типа IIB. Приводится обзор результатов, касающихся различных аспектов применения матричных моделей в непертурбативной теории струн.
Каку М. Введение в теорию суперструн / пер. с англ. Г. Э. Арутюнова, А. Д. Попова, С. В. Чудова; под ред. И. Я. Арефьевой. — М.: Мир, 1999. — 624 с. — ISBN 5-03-002518-9. — Монография в доступной форме представляет основные сведения по квантовой теории поля и теории струн, полевой теории струн и методам построения четырёхмерных струн. Снабжена приложением, в котором содержится сжатое изложение теории относительности, суперсимметрии, гравитации, даны сведения из теории групп и дифференциальной геометрии.
Кафиев Ю. Н. Аномалии и теория струн. — М.: Наука, 1991. — 245 с. — ISBN 5-02-029689-9. В монографии излагаются основы теории струн. Рассмотрены вопросы абелевых и неабелевых аномалий и связь между ними, бозонная струна, спиновая струна и суперструна Грина — Шварца, гетеротическая струна, функциональные методы, струна Полякова, двумерные конформные теории поля.
Кетов С. В. Введение в квантовую теорию струн и суперструн. — Новосибирск: Наука, 1990. — 368 с. — ISBN 5-02-029660-0. Монография представляет собой систематическое введение в предмет современной теории струн и суперструн. Дан анализ классической теории, на основе которого формулируются методы квантования. Рассмотрены струнные и суперструнные амплитуды, квантовые аномалии, сигма-модельный подход к построению низкоэнергетического эффективного действия. Специальная глава посвящена моделям гетеротических струн, включая четырёхмерные струны. Обсуждаются проблемы компактификации и феноменологии суперструн, методы полевой теории струн и суперструн.
Маршаков А. В.. Теория струн или теория поля? // УФН. — 2002. — Т. 172, № 9. — С. 977—1020. (Проверено 27 апреля 2011) — Рассматривается теория струн на определённом рубеже её развития, обсуждаются основные достижения последних лет, связанные прежде всего с попытками выхода за рамки теории возмущений как с точки зрения теории струн, так и с точки зрения квантовой теории поля. Подобный анализ помогает лучше осознать роль и место квантовой теории поля и теории струн в современной физической картине мира. Особо отмечается, что описывающей широкий круг экспериментальных явлений квантовой теории поля присущи непреодолимые внутренние проблемы, главной из которых является невозможность сформулировать на этом языке квантовую теорию гравитации.
Морозова А. Ю. Теория струн — что это такое (Проверено 27 апреля 2011) — попытка описать предмет и метод теории струн в современном понимании этого слова, то есть всю совокупность вопросов, привлекающих внимание теоретиков, работающих в этой области. Упоминается струнная модель великого объединения фундаментальных взаимодействий, но говорится и о более широком струнном сценарии единой теории поля — концепции более математического характера, нацеленной на выяснение общих свойств классов эквивалентности модельной квантовой теории поля. Приводится также краткий словарь наиболее важных терминов, необычных для физической литературы, но часто встречающихся в статьях по теории струн.
Поляков А. М. Калибровочные поля и струны. — М.: ИТФ, 1995. — 300 с. По мнению доктора физико-математических наук, заведующего лабораторией математической физики ГНЦ РФ «Институт теоретической и экспериментальной физики» А. Ю. Морозова (см. статью «Теория струн — что это такое?»), в этой монографии лучше всего отражены «методология и сам дух теории», даже в сравнении с классической монографией Грина, Шварца и Виттена и работой С. В. Кетова.- Цвибах Б. Начальный курс теории струн = Zwiebach, Barton (Second edition, 2009). A First Course in String Theory, Cambridge University Press. / Арефьева И. Я., Санюк В. И. (под ред.). Перевод с англ.: Алкалаев К. Б., Берков А. В.. — М.: URSS (Едиториал УРСС), 2011. — 784 с. — ISBN 978-5-354-01367-8.
- На английском
Becker, Katrin; Becker, Melanie; and Schwarz, John H. (2007). String Theory and M-Theory: A Modern Introduction, Cambridge University Press. ISBN 0-521-86069-5.
Headrick, Matthew (2008), "A solution manual for Polchinski's "String Theory"", arΧiv:0812.4408v1
Polchinski, Joseph (1998). String Theory, Cambridge University Press.
- Vol. 1: An introduction to the bosonic string. ISBN 0-521-63303-6.
- Vol. 2: Superstring theory and beyond. ISBN 0-521-63304-4.
Tong, David (2012), "Lectures on String Theory", arΧiv:0908.0333v3
Критика теории струн |
- Roger Penrose. The Road to Reality: A Complete Guide to the Laws of the Universe. — Knopf, 2005. — 624 с. — ISBN 0-679-45443-8.
- Lee Smolin. The Trouble with Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next. — New York: Houghton Mifflin Co., 2006. — 392 с. — ISBN 0-618-55105-0.
- Peter Woit. Not Even Wrong - The Failure of String Theory And the Search for Unity in Physical Law. — London: Jonathan Cape &: New York: Basic Books, 2006. — 290 с. — ISBN 0-224-07605-1 & ISBN 978-0-465-09275-8.
Ссылки |
Официальный сайт теории струн (англ.)
- На русском
- Гросс Д. Грядущие революции в фундаментальной физике (неизв.). Элементы.ру (2006-04-25, +видео). Проверено 17 декабря 2013. Архивировано 16 мая 2014 года.
- Иванов И. Теория суперструн: в поисках выхода из кризиса (неизв.). Элементы.ру (10 октября 2005). Проверено 17 июля 2012. Архивировано 10 февраля 2012 года.
- Левин А. Струнный концерт для Вселенной (неизв.). Популярная механика (март 2006). Проверено 17 июля 2012. Архивировано 10 февраля 2012 года.
- Пьерр Дж. М. Введение в суперструны (неизв.). Астронет (14 января 2003). Проверено 17 июля 2012. Архивировано 10 февраля 2012 года.
Семихатов А. Суперструны: на пути к теории всего (часть 1) (часть 2) // Наука и жизнь № 2-3 1997; С. 18-24, 56-64- Трефил Дж. Теория струн (неизв.). Элементы.ру (май 2006). Проверено 17 июля 2012. Архивировано 10 февраля 2012 года.
- Шварц П. Введение в суперструны (неизв.). Астронет (5 июня 2005). Проверено 17 июля 2012. Архивировано 10 февраля 2012 года.
- Шрёр Б. Теория струн и кризис в физике элементарных частиц (v3) (неизв.). ArXiv.org (28 марта 2006). Проверено 17 июля 2012. Архивировано 10 февраля 2012 года.
- На английском
ArXiv.org — Последние результаты исследований физики высоких энергий (англ.). (Проверено 17 июля 2012)
- Chalmers, Matthew. Stringscape (англ.). Physics World (22 August 2007). Проверено 17 июля 2012. Архивировано 10 февраля 2012 года.
- Schroer, Bert. String theory, the crisis in particle physics and the ascent of metaphoric arguments (v5) (англ.). ArXiv.org (26 February 2009). Проверено 17 июля 2012.
- Shellard, Paul et al. Quantum Gravity (англ.). DAMTP, University of Cambridge (1996). Проверено 17 июля 2012. Архивировано 10 февраля 2012 года.
- Woit, Peter. String Theory: An Evaluation (англ.). ArXiv.org (16 February 2001). Проверено 17 июля 2012.
z8u3QX6AyC iu4RnDYKpKW5Ij0bZEtLJbeuM DGQwNR 4T,QZhkJZI1Ywe