Шестнадцатиячейник
| Шестнадцатиячейник | |
|---|---|
 Диаграмма Шлегеля: проекция (перспектива) шестнадцатиячейника в трёхмерное пространство | |
| Тип | Правильный четырёхмерный политоп |
| Символ Шлефли | {3,3,4} |
| Ячеек | 16 |
| Граней | 32 |
| Рёбер | 24 |
| Вершин | 8 |
| Вершинная фигура | Правильный октаэдр |
Двойственный политоп | Тессеракт |

Проекция вращающегося шестнадцатиячейника в трёхмерное пространство
Пра́вильный шестнадцатияче́йник, или просто шестнадцатияче́йник[1] — один из правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гексадекахор (от др.-греч. ἕξ — «шесть», δέκα — «десять» и χώρος — «место, пространство»), четырёхмерный гиперокта́эдр (поскольку является аналогом трёхмерного октаэдра), четырёхмерный кокуб[2] (поскольку двойственен четырёхмерному гиперкубу), четырёхмерный ортоплекс.
Открыт Людвигом Шлефли в середине 1850-х годов[3]. Символ Шлефли шестнадцатиячейника — {3,3,4}.
Содержание
1 Описание
2 В координатах
3 Ортогональные проекции на плоскость
4 Метрические характеристики
5 Заполнение пространства
6 Примечания
7 Ссылки
Описание |
Ограничен 16 трёхмерными ячейками — одинаковыми правильными тетраэдрами. Угол между двумя смежными ячейками равен в точности 120∘.{displaystyle 120^{circ }.}
Его 32 двумерных грани — одинаковые правильные треугольники. Каждая грань разделяет 2 примыкающие к ней ячейки.
Имеет 24 ребра равной длины. На каждом ребре сходятся по 4 грани и по 4 ячейки.
Имеет 8 вершин. В каждой вершине сходятся по 6 рёбер, по 12 граней и по 8 ячеек. Любая вершина соединена ребром с любой другой — кроме вершины, симметричной ей относительно центра многоячейника.
Шестнадцатиячейник можно представить как две одинаковых правильных четырёхмерных пирамиды, приложенные друг к другу своими октаэдрическими основаниями, — либо как четырёхмерную дуопирамиду[en], построенную на двух квадратах.
В координатах |
Шестнадцатиячейник можно расположить в декартовой системе координат так, чтобы его 8 вершин имели координаты (±1;0;0;0),{displaystyle (pm 1;0;0;0),}


При этом сечения многоячейника 6 координатными плоскостями будут представлять собой 6 квадратов, вершины и рёбра которых — соответственно вершины и рёбра многоячейника.
Каждая из 16 ячеек многоячейника будет располагаться в одном из 16 ортантов четырёхмерного пространства.
Начало координат (0;0;0;0){displaystyle (0;0;0;0)}
Поверхность шестнадцатиячейника при этом будет геометрическим местом точек (x;y;z;w),{displaystyle (x;y;z;w),}
- |x|+|y|+|z|+|w|=1,{displaystyle |x|+|y|+|z|+|w|=1,}
а внутренность многоячейника — геометрическим место точек, для которых
- |x|+|y|+|z|+|w|<1.{displaystyle |x|+|y|+|z|+|w|<1.}
Ортогональные проекции на плоскость |



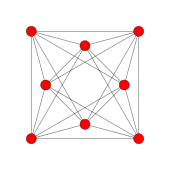

Метрические характеристики |
Если шестнадцатиячейник имеет ребро длины a,{displaystyle a,}
- V4=16a4≈0,1666667a4,{displaystyle V_{4}={frac {1}{6}};a^{4}approx 0,1666667a^{4},}
- S3=423a3≈1,8856181a3.{displaystyle S_{3}={frac {4{sqrt {2}}}{3}};a^{3}approx 1,8856181a^{3}.}
Радиус описанной трёхмерной гиперсферы (проходящей через все вершины многоячейника) при этом будет равен
- R=22a≈0,7071068a,{displaystyle R={frac {sqrt {2}}{2}};aapprox 0,7071068a,}
радиус внешней полувписанной гиперсферы (касающейся всех рёбер в их серединах) —
- ρ1=12a=0,5000000a,{displaystyle rho _{1}={frac {1}{2}};a=0,5000000a,}
радиус внутренней полувписанной гиперсферы (касающейся всех граней в их центрах) —
- ρ2=66a≈0,4082483a,{displaystyle rho _{2}={frac {sqrt {6}}{6}};aapprox 0,4082483a,}
радиус вписанной гиперсферы (касающейся всех ячеек в их центрах) —
- r=24a≈0,3535534a.{displaystyle r={frac {sqrt {2}}{4}};aapprox 0,3535534a.}
Заполнение пространства |
Шестнадцатиячейниками можно замостить четырёхмерное пространство без промежутков и наложений.
Примечания |
↑ Д. К. Бобылёв. Четырехмерное пространство // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
↑ Е. Ю. Смирнов. Группы отражений и правильные многогранники. — М.: МЦНМО, 2009. — С. 44.
↑ George Olshevsky. Hexadecachoron // Glossary for Hyperspace.
Ссылки |
Weisstein, Eric W. Шестнадцатиячейник (англ.) на сайте Wolfram MathWorld.
.mw-parser-output .ts-Родственные_проекты{background:#f8f9fa;border:1px solid #a2a9b1;clear:right;float:right;font-size:90%;margin:0 0 1em 1em;padding:.5em .75em}.mw-parser-output .ts-Родственные_проекты th,.mw-parser-output .ts-Родственные_проекты td{padding:.25em 0;vertical-align:middle}.mw-parser-output .ts-Родственные_проекты td{padding-left:.5em}
Шестнадцатиячейник на Викискладе |
| Основные выпуклые правильные и однородные политопы в размерностях 2-10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Семейство | An | Bn | I₂(p) / Dn | E₆ / E₇ / E₈ / F₄ / G₂ | H₄ | |||||||
Правильный многоугольник | Правильный треугольник | Квадрат | p-gon | Правильный шестиугольник | Правильный пятиугольник | |||||||
Однородный многогранник | Правильный тетраэдр | Правильный октаэдр • Куб | Полукуб | Правильный додекаэдр • Правильный икосаэдр | ||||||||
Однородный 4-политоп | Пятиячейник | 16-ячейник • Тессеракт | Полутессеракт | 24-ячейник | 120-ячейник • 600-ячейник | |||||||
Однородный 5-политоп | Правильный 5-симплекс | 5-ортоплекс • 5-гиперкуб | 5-полугиперкуб | |||||||||
Однородный 6-политоп | Правильный 6-симплекс | 6-ортоплекс • 6-гиперкуб | 6-полугиперкуб | 122 • 221 | ||||||||
Однородный 7-политоп | Правильный 7-симплекс | 7-ортоплекс • 7-гиперкуб | 7-полугиперкуб | 132 • 231 • 321 | ||||||||
Однородный 8-политоп | Правильный 8-симплекс | 8-ортоплекс • 8-гиперкуб | 8-полугиперкуб | 142 • 241 • 421 | ||||||||
Однородный 9-политоп | Правильный 9-симплекс | 9-ортоплекс • 9-гиперкуб | 9-полугиперкуб | |||||||||
Однородный 10-политоп | Правильный 10-симплекс | 10-ортоплекс • 10-гиперкуб | 10-полугиперкуб | |||||||||
| Однородный n-политоп | Правильный n-симплекс | n-ортоплекс • n-гиперкуб | n-полугиперкуб | 1k2 • 2k1 • k21 | n-Пятиугольный многогранник | |||||||
| Topics: Семейства политопов • Правильные политопы • Список правильных политопов и их соединений | ||||||||||||









